题目内容
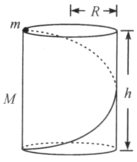
【题目】如图所示,质量为![]() 、半径为
、半径为![]() 的圆筒垂直放置在光滑水平面上,质量为
的圆筒垂直放置在光滑水平面上,质量为![]() 的小球从圆筒顶部沿圆筒内壁的螺旋槽无摩擦地下滑,筒高
的小球从圆筒顶部沿圆筒内壁的螺旋槽无摩擦地下滑,筒高![]() 正好等于螺距,即小球沿筒壁绕一周时正好到达筒底.开始时,小球和圆筒均静止不动.
正好等于螺距,即小球沿筒壁绕一周时正好到达筒底.开始时,小球和圆筒均静止不动.
(1)试分析小球下滑过程中圆筒的运动;
(2)试求小球相对地面参考系所走过的路程.
【答案】(1)小球下滑过程中圆筒的运动是筒心绕质心做半径为![]() 、角速度为
、角速度为![]() 的圆运动,同时圆筒绕筒心的转动角速度为
的圆运动,同时圆筒绕筒心的转动角速度为![]() ,“
,“![]() ”表示圆筒自转的绕行方向与系统绕质心的绕行方向相反.
”表示圆筒自转的绕行方向与系统绕质心的绕行方向相反.
(2)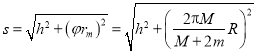
【解析】
(1)以小球与圆筒作为一个系统,初始静止,又不受水平外力作用,所以,系统质心在水平面上的投影始终不动,筒心和小球在水平方向上的运动满足动量守恒,即
![]() .
.
圆筒和小球各自运动的半径为
![]() ,
,![]() ,
,
如图乙所示.
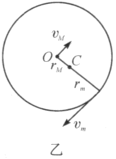
筒心和小球绕系统质心![]() 转动的角速度分别为
转动的角速度分别为
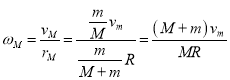 ,
,
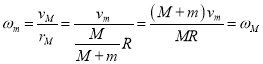 .
.
设圆筒绕筒心转动的角速度为![]() ,则由系统角动量守恒有
,则由系统角动量守恒有
![]() ,
,
即![]() .
.
所以,![]() .
.
结论:小球下滑过程中圆筒的运动是筒心绕质心做半径为![]() 、角速度为
、角速度为![]() 的圆运动,同时圆筒绕筒心的转动角速度为
的圆运动,同时圆筒绕筒心的转动角速度为![]() ,“
,“![]() ”表示圆筒自转的绕行方向与系统绕质心的绕行方向相反.
”表示圆筒自转的绕行方向与系统绕质心的绕行方向相反.
(2)先讨论小球的运动.
小球相对于地面的角速度——绝对角速度为![]() ;圆筒相对于筒心转动的角速度——相对角速度为
;圆筒相对于筒心转动的角速度——相对角速度为![]() .设小球相对于圆筒的角速度为
.设小球相对于圆筒的角速度为![]() ,则
,则
![]() ,
,
所以,![]() .
.
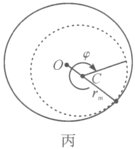
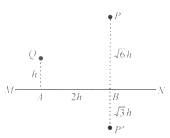
如图丙所示,设小球最终相对于地转过的角度为![]() ,则
,则
![]() ,所以
,所以![]() .
.
将小球的下滑等效为斜面模型,如图丁所示.
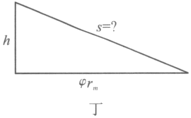
由图丁可知
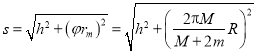 .
.
本题是角动量守恒问题中较为典型的例题,题中小球对系统质心的角动量及圆筒对系统质心的角动量都不难理解,但圆筒绕圆心转动的角动量![]() 是隐性的,很容易被忽略.
是隐性的,很容易被忽略.
此外,小球下滑的轨迹是一空间螺旋线,对其轨迹进行描述比较复杂,而选择俯视与沿圆筒柱面展开,则其轨迹特征清晰可见.
将空间问题转化为平面问题,这是一种降维思维,在处理空间问题中极为有效.至于在具体的操作中选择什么方位的投影,则需要根据自己的经验临场处理.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案