题目内容
【题目】将焦距![]() 的凸透镜从正中切去宽度为a的小部分,如图(a),再将剩下两半黏接在一起,构成一个“黏合透镜”,见图(b)。图中
的凸透镜从正中切去宽度为a的小部分,如图(a),再将剩下两半黏接在一起,构成一个“黏合透镜”,见图(b)。图中![]() ,在黏合透镜一侧的中心轴线上距镜20cm处,置一波长
,在黏合透镜一侧的中心轴线上距镜20cm处,置一波长![]() 的单色点光源S,另一侧,垂直于中心轴线放置屏幕,见图(c)。屏幕上出现干涉条纹,条纹间距
的单色点光源S,另一侧,垂直于中心轴线放置屏幕,见图(c)。屏幕上出现干涉条纹,条纹间距![]() ,试问:
,试问:

(1)切去部分的宽度a是多少?
(2)为获得最多的干涉条纹,屏幕应离透镜多远?
【答案】(1) ![]() ,(2)
,(2) ![]()
【解析】
(1)首先讨论黏合透镜的上半个透镜的成像。在图中OO是黏合透镜的中心轴线,在OO上方用实线画出了上半个透镜,在OO下方未画下半个透镜,而是补足了未切割前整个透镜的其余部分,用虚线表示。整个透镜的光轴为![]() 。
。
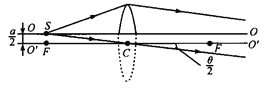
半个透镜的成像规律应与完整的透像相同。现在物点(即光源)S在黏合透镜的中心轴线上,即在
图中透镜的光轴上方![]() 处,离透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜折射后成为一束平行光束,其传播方向稍偏向下方,与光轴
处,离透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜折射后成为一束平行光束,其传播方向稍偏向下方,与光轴![]() (对OO也是一样)成角为
(对OO也是一样)成角为![]() 。当透镜完整时光束的宽度为透镜直径
。当透镜完整时光束的宽度为透镜直径![]() 透镜直径。对于上半个透就,光束宽度为
透镜直径。对于上半个透就,光束宽度为![]() 。
。

同理,S所发的光,经下半个透镜折射后,形成稍偏向上方的平行光束,与![]() 轴成
轴成![]() 角,宽度也是
角,宽度也是![]() 。
。
于是,在透镜右侧,成为夹角为![]() 的两束平行光束的干涉问题(见图),图中的两平行光束的重叠区(用阴影表示)即为干涉区。为作图清楚起见,特别是图中的
的两束平行光束的干涉问题(见图),图中的两平行光束的重叠区(用阴影表示)即为干涉区。为作图清楚起见,特别是图中的![]() 角,均远较实际角度为大。
角,均远较实际角度为大。
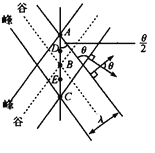
图示的是两束平行光的干涉情况,其中![]() 是和上图中的
是和上图中的![]() 相对应的。图中实线和虚线分别表示某一时刻的波峰平面和波谷平面。在垂直于中心轴线屏幕上,A、B、C表示相长干涉的亮纹位置,D、E表示相消干涉的暗纹位置,相邻波峰平面之间的垂直距离是波长λ。故干涉条纹间距
相对应的。图中实线和虚线分别表示某一时刻的波峰平面和波谷平面。在垂直于中心轴线屏幕上,A、B、C表示相长干涉的亮纹位置,D、E表示相消干涉的暗纹位置,相邻波峰平面之间的垂直距离是波长λ。故干涉条纹间距![]() 满足
满足![]() 。
。
在![]() 很小的情况下,上式成为
很小的情况下,上式成为![]() 。
。
所以透镜切去的宽度为
![]() ,
,
![]() ,果然是一个很小的角度。
,果然是一个很小的角度。
(2)由以上的求解过程可知,干涉条纹间距Δx屏幕离透镜L的距离无关,这正是两束平行光干涉的特点。但屏幕必须位于两束光的相干叠加区才行。图中以阴影菱形部分表示这一相干叠加区。因为由1式知条纹是等距的,显然当屏幕位于PQ处可获得最多的干涉条纹,而PQ平面到透镜L的距离
![]() 。
。