题目内容
【题目】某学校(110°E)地理兴趣小组在平地上用立竿测影的方法,逐日测算正午太阳高度.如图甲,垂直竖立一根2米长的竿0P,正午时测得竿影长OP′,通过tanα= ![]() ,算出正午太阳高度α.据此回答下题.
,算出正午太阳高度α.据此回答下题.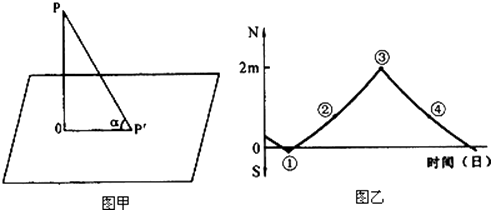
(1)该小组每天测量影长时,北京时间应为( )
A.12:00
B.12:40
C.11:20
D.11:00
(2)3月21日,当该小组进行观测时,下列城市中即将迎来旭日东升的是( )
A. 英国伦敦
B.匈牙利布达佩斯(约19°E)
C.土耳其伊斯坦布尔(约29°E)
D.夏威夷檀香山(约158°W)
(3)图乙是该小组绘制的连续一年多的竿影长度变化图.图中反映3月21日竿影长度的点是( )
A.①
B.②
C.③
D.④
(4)该学校大约位于( )
A.21.5°N
B.21.5°S
C.45°N
D.45°S
【答案】
(1)B
(2)B
(3)D
(4)A
【解析】(1)该小组每天测量影长时,当地地方时为12点,当地经度为110°E,北京时间所在经度为120°,比110°E早40分钟,根据“东早西晚、东加西减”,北京时间应为12:40.(2)A、该小组进行观测时间为当地12点,当地的经度为110°E,根据“东早西晚、东加西减”,英国伦敦时间为4点40分,故不符合题意;B、该小组进行观测时间为当地12点,当地的经度为110°E,根据“东早西晚、东加西减”,匈牙利布达佩斯(约19°E)时间大约为5点56分,即将迎来旭日东升,故正确;C、该小组进行观测时间为当地12点,当地的经度为110°E,根据“东早西晚、东加西减”,土耳其伊斯坦布尔(约29°E)时间为6点36分,已经日出,故不符合题意;D、该小组进行观测时间为当地12点,当地的经度为110°E,根据“东早西晚、东加西减”,夏威夷檀香山(约158°W)时间为18点08分,已经日落,故不符合题意.(3)读图可知,该地区一年中影长有两次可以为0的日期,即一年有两次直射,由此判断位于回归线和赤道之间;影子指向正北的时间多于向南的时间,该地位于北回归线与赤道之间;图中③时刻影子最长,为冬至日,④时刻影子在变短,为春分日,②为秋分日,影子在变长.(4)图中③时刻影子最长,为冬至日,影长为2米,首先通过冬至日竿影长度和竹竿实际长度之比是1,通过太阳高度计算公式H=90°﹣两者之间的纬度差,冬至日当地的正午太阳高度为45°,冬至日太阳直射南回归线,从而计算出纬度大约为21.5°N.
故选:(1)B.(2)B.(3)D.(4)A.