题目内容
【题目】(题文)设![]() ,圆
,圆![]() :
:![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,直线
,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
(1)用![]() 表示
表示![]() 和
和![]() ;
;
(2)求证:![]() ;
;
(3)设![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ,
,![]()
(2)根据题意,由于![]() ,
,![]()
进而得到证明。
(3) 先证:当![]() 时,
时,![]() .然后借助于不等式关系放缩法求和比较大小。
.然后借助于不等式关系放缩法求和比较大小。
【解析】试题分析:(1)根据点![]() 在圆
在圆![]() 上,在直线
上,在直线![]() 上,即可求得
上,即可求得![]() ,再利用函数的单调性即可得证
,再利用函数的单调性即可得证![]() ;(2)首先证明不等式
;(2)首先证明不等式![]() ,进而可证得
,进而可证得![]() ,累加求和即可得证.
,累加求和即可得证.
试题解析:(1)由点![]() 在曲线
在曲线![]() 上可得
上可得![]() ,又点在圆
,又点在圆![]() 上,则
上,则![]() ,
,![]() ,从而直线
,从而直线![]() 的方程为
的方程为![]() ,由点
,由点![]() 在直线
在直线![]() 上得:
上得:![]() ,将
,将![]() 代入,化简得:
代入,化简得:![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,又∵
,又∵![]() ,
,![]() ,∴
,∴![]()
![]() ;(2)先证:当
;(2)先证:当![]() 时,
时,![]() ,
,
事实上,不等式![]()
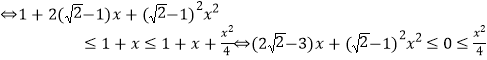 ,
,
后一个不等式显然成立,而前一个不等式![]() ,
,
故当![]() 时,不等式
时,不等式![]() 成立,
成立,
∴![]() ,∴
,∴![]() (等号仅在
(等号仅在![]() 时成立),
时成立),
求和得:![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目