题目内容
【题目】有一匀质细绳AB，长为L，A端点悬挂在天花板上，开始时A、B等高，如图1所示。将B释放，B点掉到距天花板
时将A剪断，如图2所示。问：此时起经过多长时间，绳子刚好伸直（如图3所示）？要求用质心运动定律求解。
【答案】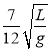
【解析】
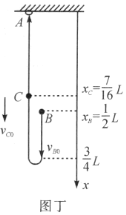
图丁是中间态
端刚好脱落时的情景，此时端速度为零，
端位置、速度以及软绳质心
的位置、速度分别为（计算略）
，
，
，
.
全绳刚好伸直时，由图丁中的几何关系易知，比朝下多走的路程为
.
其间经过时间
，因在地面参考系中，、均做具有初速的自由落体运动，即有
，解得
.
阅读解答，也许你会发出疑问，解答似乎没有用到质心运动定理啊？真的么？那么，剪断后，质心的加速度是多少？怎么来的？
的确，本题的解答过程更像是运动分析，但本模型是很容易显现出动力学特征的，如求解剪断前，天花板对绳的拉力的表达式等等.
说明一点，在学-习动量知识后，对绳子的形变产生的作用力问题，人们更习惯于运用动量定理求解作用力，但这并不能排斥质心运动定理在解答这一问题上的有效性.
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
