题目内容
已知奇函数, 的图象在x=2处的切线方程为
的图象在x=2处的切线方程为
(I )求
 的解析式;
的解析式;(II)是否存在实数,m,n使得函数
 在区间
在区间 上的最小值为m,最大值为n.若存在,求出这样一组实数m,n,若不存在,则说明理由.
上的最小值为m,最大值为n.若存在,求出这样一组实数m,n,若不存在,则说明理由.
解:(1)∵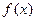 的图象关于原点对称,∴
的图象关于原点对称,∴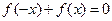 恒成立,
恒成立,
即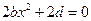 ,
,
∴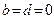 ,又
,又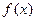 的图象在
的图象在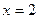 处的切线方程为
处的切线方程为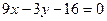 ,……2分
,……2分
∴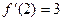 ,且
,且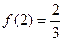 ,而
,而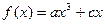 ,
,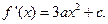
∴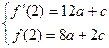 解得
解得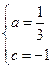
故所求的解析式为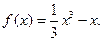 ……6分
……6分
(2)解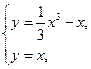 得
得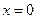 或
或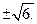
又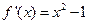 ,由
,由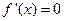 得
得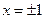 ,且当
,且当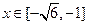 或
或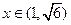 时,
时,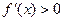 ; ……………………………………………………………………………8分
; ……………………………………………………………………………8分
当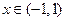 时,
时,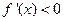 ,∴
,∴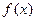 在
在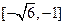 和
和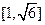 递增;在
递增;在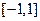 上递减
上递减
∴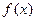 在
在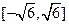 上的极大值和极小值分别为
上的极大值和极小值分别为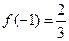 ,
,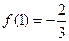 。
。
而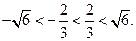
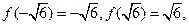
故存在这样一组实数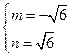 满足题意. ……………………………12分解析:
满足题意. ……………………………12分解析:
略
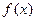 的图象关于原点对称,∴
的图象关于原点对称,∴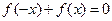 恒成立,
恒成立,即
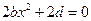 ,
,∴
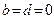 ,又
,又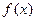 的图象在
的图象在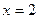 处的切线方程为
处的切线方程为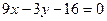 ,……2分
,……2分∴
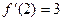 ,且
,且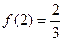 ,而
,而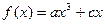 ,
,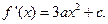
∴
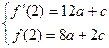 解得
解得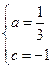
故所求的解析式为
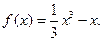 ……6分
……6分(2)解
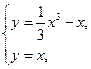 得
得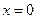 或
或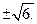
又
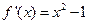 ,由
,由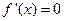 得
得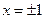 ,且当
,且当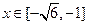 或
或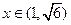 时,
时,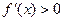 ; ……………………………………………………………………………8分
; ……………………………………………………………………………8分当
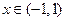 时,
时,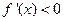 ,∴
,∴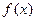 在
在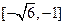 和
和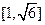 递增;在
递增;在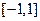 上递减
上递减∴
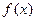 在
在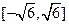 上的极大值和极小值分别为
上的极大值和极小值分别为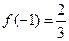 ,
,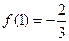 。
。而
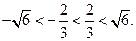
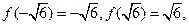
故存在这样一组实数
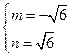 满足题意. ……………………………12分解析:
满足题意. ……………………………12分解析:略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目