题目内容
(理) 已知 ,其中
,其中 是自然常数,
是自然常数, [
[(1)讨论
 时,
时,  的单调性、极值;
的单调性、极值;(2)求证:在(Ⅰ)的条件下,
 ;
;(3)是否存在实数
 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)当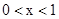 时,f(x)单调递减;当
时,f(x)单调递减;当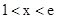 ,f(x)单调递增 ;极小值为f(1)=1 ;
,f(x)单调递增 ;极小值为f(1)=1 ;
(2)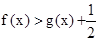 ;(3)
;(3) 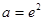 .解析:
.解析:
第一问中利用导数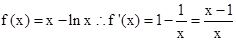 ,然后对x讨论,因为x>0,那么分为两段讨论得到函数的单调性,和极值。
,然后对x讨论,因为x>0,那么分为两段讨论得到函数的单调性,和极值。
解:(Ⅰ)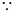
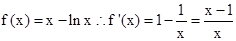 ……1分
……1分
∴当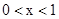 时,
时,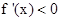 ,此时f(x)单调递减
,此时f(x)单调递减
当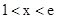 时,
时,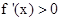 ,此时f(x)单调递增 ……3分
,此时f(x)单调递增 ……3分
∴f(x)的极小值为f(1)=1 ……4分
(Ⅱ)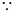 f(x)的极小值为1,即f(x)在(0,e】上的最小值为1,
f(x)的极小值为1,即f(x)在(0,e】上的最小值为1,
∴,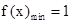 ……5分
……5分
令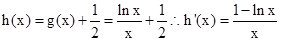 ……6分
……6分
当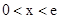 时,
时,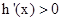 ,
,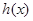 在(0,e】上单调递增 ……7分
在(0,e】上单调递增 ……7分
∴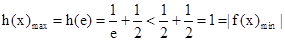
∴在(1)的条件下,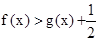 ……9分
……9分
(Ⅲ)假设存在实数a,使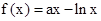 (
(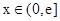 )有最小值3,
)有最小值3,
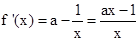 ……10分
……10分
① 当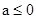 时,
时,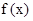 在
在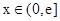 上单调递减,
上单调递减,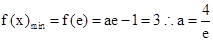 ,(舍去),所以,此时
,(舍去),所以,此时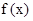 无最小值. ……12分
无最小值. ……12分
②当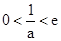 时,
时,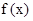 在
在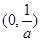 上单调递减,在
上单调递减,在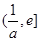 上单调递增
上单调递增
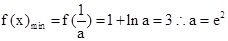 ,满足条件. ……13分
,满足条件. ……13分
③ 当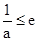 时,
时,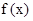 在
在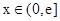 上单调递减,
上单调递减,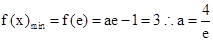 ,(舍去),所以,此时
,(舍去),所以,此时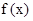 无最小值.综上,存在实数
无最小值.综上,存在实数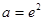 ,使得当
,使得当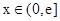 时
时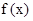 有最小值3.
有最小值3.
…………………………………………………………………………………………………….14分
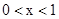 时,f(x)单调递减;当
时,f(x)单调递减;当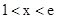 ,f(x)单调递增 ;极小值为f(1)=1 ;
,f(x)单调递增 ;极小值为f(1)=1 ;(2)
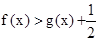 ;(3)
;(3) 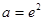 .解析:
.解析:第一问中利用导数
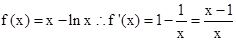 ,然后对x讨论,因为x>0,那么分为两段讨论得到函数的单调性,和极值。
,然后对x讨论,因为x>0,那么分为两段讨论得到函数的单调性,和极值。解:(Ⅰ)
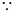
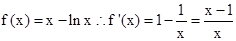 ……1分
……1分∴当
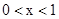 时,
时,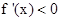 ,此时f(x)单调递减
,此时f(x)单调递减当
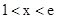 时,
时,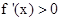 ,此时f(x)单调递增 ……3分
,此时f(x)单调递增 ……3分∴f(x)的极小值为f(1)=1 ……4分
(Ⅱ)
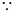 f(x)的极小值为1,即f(x)在(0,e】上的最小值为1,
f(x)的极小值为1,即f(x)在(0,e】上的最小值为1,∴,
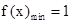 ……5分
……5分令
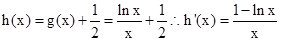 ……6分
……6分当
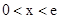 时,
时,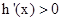 ,
,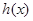 在(0,e】上单调递增 ……7分
在(0,e】上单调递增 ……7分∴
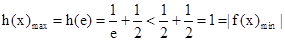
∴在(1)的条件下,
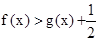 ……9分
……9分(Ⅲ)假设存在实数a,使
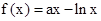 (
(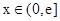 )有最小值3,
)有最小值3,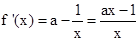 ……10分
……10分① 当
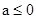 时,
时,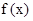 在
在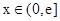 上单调递减,
上单调递减,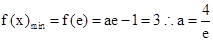 ,(舍去),所以,此时
,(舍去),所以,此时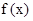 无最小值. ……12分
无最小值. ……12分②当
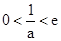 时,
时,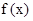 在
在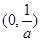 上单调递减,在
上单调递减,在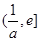 上单调递增
上单调递增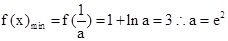 ,满足条件. ……13分
,满足条件. ……13分③ 当
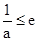 时,
时,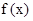 在
在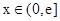 上单调递减,
上单调递减,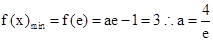 ,(舍去),所以,此时
,(舍去),所以,此时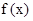 无最小值.综上,存在实数
无最小值.综上,存在实数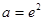 ,使得当
,使得当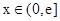 时
时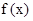 有最小值3.
有最小值3. …………………………………………………………………………………………………….14分

练习册系列答案
相关题目