题目内容
 (2012?枣庄)如图所示,工人用滑轮组缓慢地打捞沉没在水中的重物,当重物全部在水中时,拉力F为160N,滑轮组的机械效率为80%.当重物离开水面后拉力F′为480N,整个装置的摩擦和绳重不计.求:
(2012?枣庄)如图所示,工人用滑轮组缓慢地打捞沉没在水中的重物,当重物全部在水中时,拉力F为160N,滑轮组的机械效率为80%.当重物离开水面后拉力F′为480N,整个装置的摩擦和绳重不计.求:(1)动滑轮的重力;
(2)物体的重力;
(3)重物的密度.
分析:(1)已知机械效率,找出有用功和总功,根据η=
,求出滑轮组对物体的拉力,即G-F浮.
当物体浸没在水中,知道绳子自由端的拉力、滑轮组对物体的拉力,根据F=
(G-F浮+G动),求出动滑轮的重力.
(2)当物体离开水面时,知道绳子自由端的拉力和动滑轮的重力,根据F=
(G+G动),求出物体的重力.
(3)知道滑轮组对物体的拉力,即G-F浮,又知道物体的重力,求出物体浸没在水中时受到的浮力,根据阿基米德原理求出物体的体积.然后根据G=ρgV,求出物体的密度.
| W有 |
| W总 |
当物体浸没在水中,知道绳子自由端的拉力、滑轮组对物体的拉力,根据F=
| 1 |
| n |
(2)当物体离开水面时,知道绳子自由端的拉力和动滑轮的重力,根据F=
| 1 |
| n |
(3)知道滑轮组对物体的拉力,即G-F浮,又知道物体的重力,求出物体浸没在水中时受到的浮力,根据阿基米德原理求出物体的体积.然后根据G=ρgV,求出物体的密度.
解答:解:(1)设物体浸没在水中,上升h,有两段绳子承担物体的重,所以绳子自由端移动2h,
∵整个装置的摩擦和绳重不计.
∴根据η=
得:
η=
=
=
,
所以,G-F浮=2Fη=2×160N×80%=256N.
又∵F=
(G-F浮+G动)=
(G-F浮+G动),
∴G动=2F-(G-F浮)=2×160N-256N=64N.
(2)当物体离开水面时,因为,F'=
(G+G动)=
(G+G动),
所以,G=2F′-G动=2×480N-64N=896N.
(3)因为G-F浮=256N,即:896N-1.0×103kg/m3×10N/kg×V=256N,
所以,V=6.4×10-2m3.
根据G=mg=ρVg,
所以ρ=
=
=1.4×103kg/m3.
答:(1)动滑轮的重力为64N;
(2)物体的重力为896N;
(3)重物密度为1.4×103kg/m3.
∵整个装置的摩擦和绳重不计.
∴根据η=
| W有 |
| W总 |
η=
| W有 |
| W总 |
| (G-F浮)h |
| F×2h |
| G-F浮 |
| 2F |
所以,G-F浮=2Fη=2×160N×80%=256N.
又∵F=
| 1 |
| n |
| 1 |
| 2 |
∴G动=2F-(G-F浮)=2×160N-256N=64N.
(2)当物体离开水面时,因为,F'=
| 1 |
| n |
| 1 |
| 2 |
所以,G=2F′-G动=2×480N-64N=896N.
(3)因为G-F浮=256N,即:896N-1.0×103kg/m3×10N/kg×V=256N,
所以,V=6.4×10-2m3.
根据G=mg=ρVg,
所以ρ=
| G |
| Vg |
| 896N |
| 6.4×10-2m3×10N/kg |
答:(1)动滑轮的重力为64N;
(2)物体的重力为896N;
(3)重物密度为1.4×103kg/m3.
点评:本题涉及到机械效率、阿基米德原理、使用滑轮组时绳子自由端和重物的关系等,综合性很强,有很大的难度.

练习册系列答案
相关题目
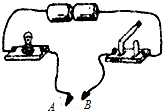 (2012?枣庄)如图所示电路,把两个金属夹子A、B夹在下列某个学习用品的两端(物体保持干燥),闭合开关后小灯泡能发光的是( )
(2012?枣庄)如图所示电路,把两个金属夹子A、B夹在下列某个学习用品的两端(物体保持干燥),闭合开关后小灯泡能发光的是( ) (2012?枣庄)如图所示的是为纪念发现“磁生电”现象的物理学家法拉第而发行的一枚邮票,该发现导致了世界上第一台
(2012?枣庄)如图所示的是为纪念发现“磁生电”现象的物理学家法拉第而发行的一枚邮票,该发现导致了世界上第一台 (2012?枣庄)如图所示,物体甲静止在水平地面上,对地面的压强是5.4×105Pa.有一重力可忽略不计杠杆AB,支点为0,且OA:0B=2:1.将甲挂在杠杆的B端,在A端施50N竖直向下的拉力时,杠杆在水平位置平衡,此时物体甲对地面的压强变为1.8×105Pa.当物体甲对地面的压力刚好为零时,在杠杆A端应施
(2012?枣庄)如图所示,物体甲静止在水平地面上,对地面的压强是5.4×105Pa.有一重力可忽略不计杠杆AB,支点为0,且OA:0B=2:1.将甲挂在杠杆的B端,在A端施50N竖直向下的拉力时,杠杆在水平位置平衡,此时物体甲对地面的压强变为1.8×105Pa.当物体甲对地面的压力刚好为零时,在杠杆A端应施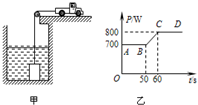 (2012?枣庄)如图甲所示是使用汽车打捞水下重物的示意图.汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度v=0.2m/s向右运动.如图乙所示是此过程中汽车拉动重物的功率P随时间t变化的图象.设t=0时汽车开始提升重物,忽略水的阻力和滑轮的摩擦,(g取10N/kg),则圆柱形重物的密度是
(2012?枣庄)如图甲所示是使用汽车打捞水下重物的示意图.汽车通过定滑轮牵引水下一个圆柱形重物,在整个打捞过程中,汽车以恒定的速度v=0.2m/s向右运动.如图乙所示是此过程中汽车拉动重物的功率P随时间t变化的图象.设t=0时汽车开始提升重物,忽略水的阻力和滑轮的摩擦,(g取10N/kg),则圆柱形重物的密度是