题目内容
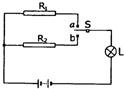 如图所示R1和R2为两个定值电阻,R2是R1的n倍,小灯泡L上标有“6V 3W”的字样,s为单刀双掷开关.当S与点a接通时,小灯泡正常发光;当S与点b接通时,小灯泡消耗的功率为额定功率的四分之一.
如图所示R1和R2为两个定值电阻,R2是R1的n倍,小灯泡L上标有“6V 3W”的字样,s为单刀双掷开关.当S与点a接通时,小灯泡正常发光;当S与点b接通时,小灯泡消耗的功率为额定功率的四分之一.(1)若n为小于5的正整数,试通过计算说明n的可能值.
(2)试求n取以上可能值时,R1和R2相应的阻值.
分析:(1)由灯泡铭牌可利用功率公式求得小灯泡的电阻及灯泡的额定功率.由S接a和b时的功率关系可得出电流关系,则由欧姆定律及前后的电流关系可得出R1的表达式,由表达式通过分析题干中的条件可得出n可能的值;
(2)由第一问中求得的n的可能值,列出两次的功率方程即可求得两电阻的阻值.
(2)由第一问中求得的n的可能值,列出两次的功率方程即可求得两电阻的阻值.
解答:解:由P=UI得
灯泡的额定电流为I=
=
=0.5A.
由I=
得:
小灯泡的电阻R=
=
=12Ω.
当开关接b时,灯泡的实际功率为P实=
P=
W
则由功率公式可得:I实=
=
=
A
由欧姆定律可得:
I=
-----(1)
I实=
----(2)
R2=nR1
将(1)与(2)作比得:
=
代入得:2=
化简得:(n-2)R1=12Ω
因n只能取小于5的正整数,且R1为正值,要保证上式成立,n只能取3或4.
(2)当n取3时,由(n-2)R1=12得:
R1=12Ω,R2=nR1=3×12Ω=36Ω;
当n取4时,由(n-2)R1=12得:
R1=6Ω,R2=4R1=4×6Ω=24Ω.
答:(1)n可能为3或4;
(2)当n为3时,R1为12Ω,R2为36Ω;当n为4时,R1为6Ω,R2为24Ω.
灯泡的额定电流为I=
| P |
| U |
| 3W |
| 6V |
由I=
| U |
| R |
小灯泡的电阻R=
| U |
| I |
| 6V |
| 0.5A |
当开关接b时,灯泡的实际功率为P实=
| 1 |
| 4 |
| 3 |
| 4 |
则由功率公式可得:I实=
|
|
| 1 |
| 4 |
由欧姆定律可得:
I=
| U |
| R1+R |
I实=
| U |
| R2+R |
R2=nR1
将(1)与(2)作比得:
| I |
| I实 |
| R2+R |
| R1+R |
代入得:2=
| nR1+12Ω |
| R1+12Ω |
化简得:(n-2)R1=12Ω
因n只能取小于5的正整数,且R1为正值,要保证上式成立,n只能取3或4.
(2)当n取3时,由(n-2)R1=12得:
R1=12Ω,R2=nR1=3×12Ω=36Ω;
当n取4时,由(n-2)R1=12得:
R1=6Ω,R2=4R1=4×6Ω=24Ω.
答:(1)n可能为3或4;
(2)当n为3时,R1为12Ω,R2为36Ω;当n为4时,R1为6Ω,R2为24Ω.
点评:对需要计论的问题,很多同学感到无从下手.其实只要细心审题,利用题目中给出的相关知识利用数学规律列出方程式,对可能的情况进行分析即可求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 下表为某电烤箱铭牌的部分参数,其简化电路如图所示R1、R2均为电热丝.求
下表为某电烤箱铭牌的部分参数,其简化电路如图所示R1、R2均为电热丝.求
 如图所示R1和R2为两个定值电阻,R2是R1的n倍,小灯泡L上标有“6V 3W”的字样,s为单刀双掷开关.当S与点a接通时,小灯泡正常发光;当S与点b接通时,小灯泡消耗的功率为额定功率的四分之一.
如图所示R1和R2为两个定值电阻,R2是R1的n倍,小灯泡L上标有“6V 3W”的字样,s为单刀双掷开关.当S与点a接通时,小灯泡正常发光;当S与点b接通时,小灯泡消耗的功率为额定功率的四分之一.