题目内容
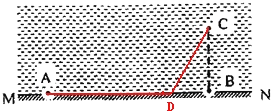
【题目】设湖岸MN为一直线，在岸边的A点的游客发现湖中C点处有人落水，此时C点离湖岸最近点为B点，BC距离为60米，AB距离为80米，游客从A点出发去营救落水者。已知人在岸上走的速度为v1=5m/s，在水中游泳的速度为v2=3m/s．此游客从A点到达C点最少用时为
A. 36s B. 
C. 32s D. 28s
【答案】C
【解析】
设AB上有一点D，游客沿A→D→C时，所用的时间最短，
设BD的距离为s，AD的距离为80ms，CD的距离为
，由v＝
可得，游客从A点到达C点的时间：t＝
+
＝16s+
(53s)，取y＝53x，则(y+3x)2＝25(x2+602)，整理可得：16x26yx+(25×602y2)＝0，因方程有解，所以,△＝(6y)24×16×(25×602y2)0，解得：y240，则t16s+
＝32s.故选C.
练习册系列答案
特高级教师点拨系列答案
相关题目
【题目】小丽家新买了一台电热水器，下表是该热水器的一些技术参数．现将水箱中装满水，通电后正常工作40min，水温从25℃上升到45℃，（c水=4.2×103J/（kg℃）
型号 | FED﹣H50 | 额定电压 | 220V |
最大水量 | 50kg | 额定功率 | 2000W |
求：
（1）此过程中水所吸收的热量；
（2）热水器中电热丝的电阻；
（3）热水器的效率．
