题目内容
【题目】底面积不同的圆柱形容器A和B原先分别盛有体积相同的甲、乙两种液体，如图所示，现从容器中分别抽出部分液体后，液体对各自容器底部的压强为p甲、p乙 ， 则下列做法中，符合实际的是（ ）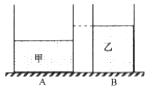 
A.若液体原先对容器底部的压力相等，则抽出相等质量的液体后，p甲一定等于p乙
B.若液体原先对容器底部的压力相等，则抽出相等厚度的液体后，p甲可能大于p乙
C.若液体原先对容器底部的压强相等，则抽出相等体积的液体后，p甲一定等于p乙
D.若液体原先对容器底部的压强相等，则抽出相等厚度的液体后，p甲一定等于p乙
【答案】C
【解析】解： A、假设液体原先对容器底部的压力相等即 
= 
，由图可知，S甲＞S乙 ， 由p= 
可知，液体原先对容器底部的压强 
＜ 
，
抽出相等质量的液体后，液体对各自容器底部的压力为F甲=F乙 ， 已知S甲＞S乙 ， 由p= 可知，液体对各自容器底部的压强为p甲＜p乙 ， 故A错误；
B、若液体原先对容器底部的压力相等，则抽出相等厚度的液体后，假如抽取甲容器中全部液体的厚度，则由p= = 
= 
= 
=ρgh可知，p甲为0，p乙大于0，故B错误；
C、若液体原先对容器底部的压强相等，即 = ，已知V甲=V乙 ， 则由p=ρgh可得， =ρ甲g 
， =ρ乙g 
，
即ρ甲g =ρ乙g ，
由此可得，ρ甲g 
=ρ乙g 
，
抽出相等体积的液体V后，则V剩甲=V甲﹣V，则V剩乙=V乙﹣V，
则V剩甲=V剩乙 ，
则p甲=ρ甲g 
=ρ甲g ×V剩甲 ， p乙=ρ乙g 
=ρ乙g ×V剩乙 ，
所以p甲=ρ乙 ， 故C正确；
D、若液体原先对容器底部的压强相等，即 = ，则ρ甲gh甲=ρ乙gh乙 ，
已知h甲＜h乙 ，
所以ρ甲＞ρ乙 ，
则抽出相等厚度的液体后，p甲=ρ甲g（h甲﹣h）=ρ甲gh甲﹣ρ甲gh，
p乙=ρ乙g（h乙﹣h）=ρ乙gh乙﹣ρ乙gh，
则p甲＜p乙 ． 故D错误．
故选C．
【考点精析】本题主要考查了压强的大小及其计算的相关知识点，需要掌握压强的计算公式及单位：公式：p =F/s ,p表示压强，F表示压力，S表示受力面积压力的单位是 N，面积的单位是 m2, 压强的单位是 N/m2,叫做帕斯卡，记作Pa ．1Pa=1N/m2．(帕斯卡单位很小，一粒平放的西瓜子对水平面的压强大约为20Pa）才能正确解答此题．
