��Ŀ����
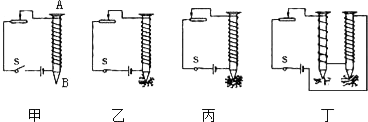
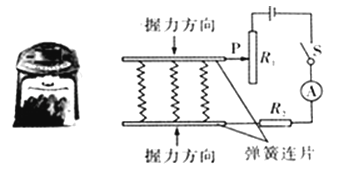
����Ŀ����ͼ����ʾ������ˮƽ�����ϵ�Բ���������ĵ����Ϊ100cm2 �� װ��20cm���ˮ������������Ϊ0.02kg����Ⱥ��Բ��ƣ�A��B�����ܶȲ�ͬ�IJ����Ƴɵ���ʵ����飬��֪B���������A�������� ![]() ������A��B�������ϸ����������ˮ��ʱ�������ǡ����������û��ˮ�������ͼ����ʾ���ּ���ϸ�ߣ�A����ϸ����ȶ���ˮ��������ѹǿ�仯��60Pa�����A��
������A��B�������ϸ����������ˮ��ʱ�������ǡ����������û��ˮ�������ͼ����ʾ���ּ���ϸ�ߣ�A����ϸ����ȶ���ˮ��������ѹǿ�仯��60Pa�����A�� ![]() ���¶��ˮ�森��֪ˮ���ܶ�Ϊ1.0��103kg/m3 �� gȡ10N/kg������
���¶��ˮ�森��֪ˮ���ܶ�Ϊ1.0��103kg/m3 �� gȡ10N/kg������ 
��1����ͼ����ʾ��������ˮƽ�����ѹǿ��
��2��ϸ�߱����Ϻ�ˮ��ĸ߶Ȳ
��3��A��B�������ܶȣ�
���𰸡�
��1���⣺Բ����������ˮ�������
Vˮ=S��hˮ=100cm2��20cm=2000cm3��
�ɦ�= ![]() �ɵã�ˮ��������
�ɵã�ˮ��������
mˮ=��ˮVˮ=1.0g/cm3��2000cm3=2000g=2kg��
������ˮƽ�����ѹ����
F=G��=��m��+mˮ��g=��0.02kg+2kg����10N/kg=20.2N��
������ˮƽ�����ѹǿ��
p= ![]() =
= ![]() =2020Pa��
=2020Pa��
����ͼ����ʾ��������ˮƽ�����ѹǿΪ2020Pa��
��2���⣺��p=��gh�ɵã�ϸ�߱����Ϻ�ˮ��ĸ߶Ȳ
��h= ![]() =
= ![]() =6��10��3m=0.6cm��
=6��10��3m=0.6cm��
��ϸ�߱����Ϻ�ˮ��ĸ߶Ȳ�Ϊ0.6cm��
��3���⣺ϸ�߱����Ϻ�AƯ�������A�� ![]() ���¶��ˮ�棬��V��A=
���¶��ˮ�棬��V��A= ![]() VA��
VA��
������Ư��ʱ�ܵ��ĸ�����������������ȣ�
���ԣ���F��=��gV����G=mg=��Vg�ɵã�
��ˮgV��A=��AVAg��
���A= ![]() ��ˮ=
��ˮ= ![]() ��1.0��103kg/m3=0.75��103kg/m3��
��1.0��103kg/m3=0.75��103kg/m3��
���A�� ![]() ���¶��ˮ�棬��A¶��ˮ�������������ڼ���ˮ�������ȣ���
���¶��ˮ�棬��A¶��ˮ�������������ڼ���ˮ�������ȣ��� ![]() VA=S����h��
VA=S����h��
������A�������
VA=4S����h=4��100cm2��0.6cm=240cm3��VB= ![]() VA=
VA= ![]() ��240cm3=30cm3��
��240cm3=30cm3��
����ϸ��ǰ��AB�����ǡ����������
��ˮg��VA+VB��=��AVAg+��BVBg��
B������ܶȣ�
��B= ![]() ��ˮ��
��ˮ�� ![]() ��A=
��A= ![]() ��1.0��103kg/m3��
��1.0��103kg/m3�� ![]() ��0.75��103kg/m3=3��103kg/m3��
��0.75��103kg/m3=3��103kg/m3��
��A�����ܶ�Ϊ0.75��103kg/m3��B�����ܶ�Ϊ3��103kg/m3��
����������1������V=Sh���Բ����������ˮ����������ݦ�= ![]() ���ˮ��������������ˮƽ�����ѹ������������ˮ������֮�ͣ�����F=G=mg������С������p=
���ˮ��������������ˮƽ�����ѹ������������ˮ������֮�ͣ�����F=G=mg������С������p= ![]() ���������ˮƽ�����ѹǿ����2��֪������ϸ�ߺ�ˮ��������ѹǿ�仯��������p=��gh���ϸ�߱����Ϻ�ˮ��ĸ߶Ȳ��3��ϸ�߱����Ϻ�AƯ���������A��
���������ˮƽ�����ѹǿ����2��֪������ϸ�ߺ�ˮ��������ѹǿ�仯��������p=��gh���ϸ�߱����Ϻ�ˮ��ĸ߶Ȳ��3��ϸ�߱����Ϻ�AƯ���������A�� ![]() ���¶��ˮ������ſ�ˮ�����������Ư��������F��=��ҺgV����G=mg=��Vg�ó���ʽ�������A���ܶȣ����A��
���¶��ˮ������ſ�ˮ�����������Ư��������F��=��ҺgV����G=mg=��Vg�ó���ʽ�������A���ܶȣ����A�� ![]() ���¶��ˮ�棬��A¶��ˮ�������������ڼ���ˮ�������ȣ��ݴ����A���������һ�����B�����������ϸ��ǰ��AB�����ǡ������������F��=��ҺgV����G=mg=��Vg�ó���ʽ�������B������ܶȣ�
���¶��ˮ�棬��A¶��ˮ�������������ڼ���ˮ�������ȣ��ݴ����A���������һ�����B�����������ϸ��ǰ��AB�����ǡ������������F��=��ҺgV����G=mg=��Vg�ó���ʽ�������B������ܶȣ�
�����㾫����������Ĺؼ���������ѹǿ�Ĵ�С�����������֪ʶ������ѹǿ�ļ��㹫ʽ����λ����ʽ��p =F/s ,p��ʾѹǿ��F��ʾѹ����S��ʾ�������ѹ���ĵ�λ�� N������ĵ�λ�� m2, ѹǿ�ĵ�λ�� N/m2,������˹��������Pa ��1Pa=1N/m2��(��˹����λ��С��һ��ƽ�ŵ������Ӷ�ˮƽ���ѹǿ��ԼΪ20Pa�����Լ�������ԭ�������⣬�˽Ⱒ����ԭ��������Һ���е������ܵ����ϵĸ����������Ĵ�С���������ſ���Һ�����ܵ�������������ɽ���������ԭ������ F��= G�� =��Һgv����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��С��ͬѧ�������ͼ����ʾ������ת��ָʾ�Ƶ�·ģ�ͣ���ͨ��Ӧָʾ�ƺ�ָʾ�ƻ��������������⣩������˸���⣬��·�е�Դ��ѹ��Ϊ6V��R0Ϊ��ֵ���裬ָʾ�ƹ���Ϊ��6V 3W�����������Ȧ�������ĵ�����Բ��ƣ�ָʾ�Ƶĵ�ѹ������ı仯���������ʾ��
��ѹ/V | �� | 0.5 | 1.2 | 2.0 | 3.0 | 4.0 | 5.0 | 5.5 | �� |
����/A | �� | 0.08 | 0.12 | 0.18 | 0.26 | 0.34 | 0.42 | 0.46 | �� |
��1��������ת����תָʾ��ͬʱ������ת��Ӧ�봥����ͨ��ѡ�1��2������2��3������3��4����4��5������ 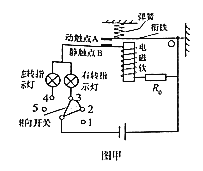
��2����ת���봥�㡰2��3����ͨʱ����תָʾ������ʵ�ʵ�ѹU����ʱ��t�仯������ͼ����ʾ����֪����תָʾ��������ʱ����תָʾ�ƵĹ����붨ֵ����R0�Ĺ���֮����1��4����ֵ����R0����ֵ�� 
��3����תָʾ�ƽ�����˸����15sʱ����ָʾ�ƺ�R0���ĵĵ��ֱܷ��Ƕ��٣�