Question

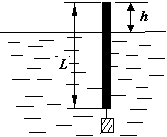
一根均匀的木棍长度为L，密度为ρ₁．下挂一个质量为m的小金属块后，能如图所示漂浮在密度为ρ₂的液体中．此时木棍露出液面的长度为h．用剪刀剪掉长度为L'=    的木棍，剩余的木棍和金属块恰能悬浮在原来的液体中．

Answer 1

【答案】分析：分两种状态分析：一、原来漂浮，根据漂浮条件列出受到浮力等于重力的关系式；二、剪掉L′后的悬浮，根据悬浮条件列出受到浮力等于重力的关系式；联立方程求解．
解答：解：设木棒横截面积为s，小金属块在液体中受到的浮力为F_金，
小金属块的受到重力：G_金=mg，
∵原来木棒漂浮在液体中，
∴F_浮=G，
即：ρ₂（L-h）sg+F_金=G_金+ρ₁Lsg，--------①
∵剪掉L′后，木棒悬浮在液体中，
∴F_浮′=G′，
即：ρ₂（L-L′）sg+F_金=G_金+ρ₁（L-L′）sg，--------②
由①-②得：
ρ₂（L-h）sg-ρ₂（L-L′）sg=ρ₁Lsg-ρ₁（L-L′）sg，
解得：L′=h．
故答案为：h．
点评：本题关键：一是漂浮、悬浮条件的使用，二是两种情况下小金属块受到的重力和浮力大小不变（隐含条件）．