题目内容
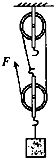 (2003?南昌)如图所示的装置中,滑轮组的机械效率为80%,货物重为400N.若用力F把货物匀速提升2m.求:
(2003?南昌)如图所示的装置中,滑轮组的机械效率为80%,货物重为400N.若用力F把货物匀速提升2m.求:(1)提升货物时做的有用功;
(2)F所做的总功及额外功;
(3)F的大小.
分析:(1)克服物体重力做的功为有用功,根据公式W=Gh可求.
(2)已知机械效率和有用功,根据公式η=
可求总功,额外功等于总功减去有用功.
(3)已知总功和物体提升的高度以及动滑轮上绳子的段数,根据公式W=FS可求拉力的大小.
(2)已知机械效率和有用功,根据公式η=
| W有用 |
| W总 |
(3)已知总功和物体提升的高度以及动滑轮上绳子的段数,根据公式W=FS可求拉力的大小.
解答:解:(1)W有用=Gh=400N×2m=800J;
(2)∵η=
∴W总=
=
=1000J,
所以W额=W总-W有用=1000J-800J=200J;
(3)拉力F=
=
≈166.67N.
答:(1)工人提升货物时做的有用功为800J;
(2)工人所做额外功为200J;
(3)工人所用拉力F的大小为166.67N.
(2)∵η=
| W有用 |
| W总 |
∴W总=
| W有用 |
| η |
| 800J |
| 80% |
所以W额=W总-W有用=1000J-800J=200J;
(3)拉力F=
| W总 |
| S |
| 1000J |
| 3×2m |
答:(1)工人提升货物时做的有用功为800J;
(2)工人所做额外功为200J;
(3)工人所用拉力F的大小为166.67N.
点评:本题考查有用功、总功、额外功、机械效率的计算以及四者之间的关系和机械效率公式的灵活应用,本题的关键是分清动滑轮上绳子的段数.

练习册系列答案
相关题目
 (2003?南昌)如图所示电路中,当S1、S3断开,S2闭合时,L1与L2
(2003?南昌)如图所示电路中,当S1、S3断开,S2闭合时,L1与L2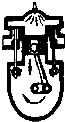

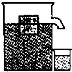 (2003?南昌)如图,将边长为a的实心正方体木块轻轻放入装满水的溢水杯中,设水的密度为ρ水.木块静止时,从杯中溢出水的质量为m,根据以上条件,求出五个与木块相关的物理量(木块面积、体积除外)
(2003?南昌)如图,将边长为a的实心正方体木块轻轻放入装满水的溢水杯中,设水的密度为ρ水.木块静止时,从杯中溢出水的质量为m,根据以上条件,求出五个与木块相关的物理量(木块面积、体积除外)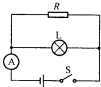 (2003?南昌)如图所示,电源电压保持不变,电阻R与灯泡L并联,R的电阻为12Ω,灯泡L的阻值为6Ω.开关S闭合后,电流表的示数为3A.求:
(2003?南昌)如图所示,电源电压保持不变,电阻R与灯泡L并联,R的电阻为12Ω,灯泡L的阻值为6Ω.开关S闭合后,电流表的示数为3A.求: