Question

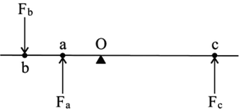一根重量可忽略不计的杠杆以O点为支点，在杆上的a、b、c三处分别受到F_a、F_b、F_c三个方向与杠杆垂直的力作用，且a、b、c三处到O点的距离比为1：2：3，如图所示．若不考虑杠杆与支点间的摩擦力，当杠杆所受到的合力矩为零时，则F_a：F_b：F_c可能为下列何者

1. A.
   1：1：3
2. B.
   1：1：5
3. C.
   3：1：1
4. D.
   5：1：1

Answer 1

D
分析：由题知，a、b、c三处到O点的距离比为1：2：3，F_a、F_b、F_c方向与杠杆垂直，可得三力的力臂关系；进而得出三力的力矩关系，由于杠杆所受到的合力矩为零，可得F_aL=2F_bL+3F_cL；再结合各个选项的力的关系分析判断．
解答：
由题知，a、b、c三处到O点的距离比为1：2：3，
设F_a的力臂为L，则F_b的力臂为2L，F_c的力臂为3L，
F_a的力矩为F_aL，则F_b的力矩为2F_bL，F_c的力矩为3F_cL，
∵杠杆所受到的合力矩为零，
∴F_aL=2F_bL+3F_cL；
A、若F_a：F_b：F_c=1：1：3，代入F_aL=2F_bL+3F_cL，该式不成立，故A错；
B、若F_a：F_b：F_c=1：1：5，代入F_aL=2F_bL+3F_cL，该式不成立，故B错；
C、若F_a：F_b：F_c=3：1：1，代入F_aL=2F_bL+3F_cL，该式不成立，故C错；
D、若F_a：F_b：F_c=5：1：1，代入F_aL=2F_bL+3F_cL，该式成立，故D正确．
故选D．
点评：本题考查了学生对杠杆平衡条件的掌握和运用，根据提供条件和杠杆所受到的合力矩为零得出F_aL=2F_bL+3F_cL是本题的关键．