Question

（2012?海淀区二模）将一轻质弹簧的两端分别固定在正方体物体A、B表面的中央，把正方体物体B放在水平桌面上，当物体A、B静止时，弹簧的长度比其原长缩短了5cm，如图甲所示．现将物体A、B 上下倒置，并将它们放入水平桌面上的平底圆柱形容器内，使物体A与容器底接触（不密合），再向容器中缓慢倒入一定量的某种液体，待物体A、B静止时，物体B上表面与液面平行，且有

1

4

的体积露出液面，此时容器底对物体A的支持力为1N．已知物体A、B的边长分别为5cm、10cm，物体A、B的密度之比为16：1，圆柱形容器的底面积为150cm²，弹簧原长为10cm，弹簧所受力F的大小与弹簧的形变量△x（即弹簧的长度与原长的差值的绝对值）的关系如图乙所示．上述过程中弹簧始终在竖直方向伸缩，且撤去其所受力后，弹簧可以恢复原长．不计弹簧的体积及其所受的浮力，g取10N/kg，则容器内倒入液体的质量是

4.84

kg．

Answer 1

分析：根据弹簧所受力F的大小与弹簧的形变量△x和弹簧的缩短量求出物体A的重力和质量，进而可求物体A、B的密度；
然后分别分析A、B的受力情况，列出关于合力为零的等式，求出弹簧对物体的拉力求出浮力，

解答：解：由图乙可知：弹簧所受力F的大小与弹簧的形变量△x的关系式是2N/cm，则弹簧的长度比其原长缩短了5cm时弹簧的压力为5cm×2N/cm=10N，则G_A=10N，
∵V_A=L_A³=（0.05m）³=1.25×10^-4m³，
根据密度公式得：ρ_A=

GA

VAg

=

10N

1.25×10-4m3×10N/kg

=8000kg/m³，
∵ρ_A：ρ_B=16：1，
∴ρ_B=

1

16

ρ_A=

1

16

×8×10³kg/m³=500kg/m³，
∵V_B =L_B³=（0.1m）³=1×10^-3m³，
∴G_B=ρ_B gV_B=500kg/m³×10N/kg×1×10^-3m³=5N，
当将物体A、B上下倒置放入容器中，则A、B受力分析如图：

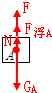
则：G_A=N+F+F_浮A-------①
G_B+F=F_浮B-------------②
解得：F_浮A+F_浮B=G_A+G_B-N=10N+5N-1N=14N，
∵待物体A、B静止时，物体B上表面与液面平行，且有

1

4

的体积露出液面，
∴V_排=V_A+（1-

1

4

）V_B=1.25×10^-4m³+（1-

1

4

）×1×10^-3m³=8.75×10^-4m³，
∵F_浮A+F_浮B=ρ_液gV_排，
则ρ_液=

F浮A+F浮B

V排g

=

14N

8.75×10-4m3×10N/kg

=1.6×10³kg/m³，
由①式得：∴F=G_A-N-F_浮A=G_A-N-ρ_液gV_A=10N-1N-1.6×10³kg/m³×10N/kg×1.25×10^-4m³=7N，
根据弹簧所受力F的大小与弹簧的形变量△x的关系式是2N/cm，则弹簧的压力为7N，则弹簧的伸长△L=3.5cm；
则液体的深度为h=L_A+L+△L+（1-

1

4

）L_B=5cm+10cm+3.5cm+（1-

1

4

）×10cm=26cm=0.26m，
V_液=sh-V_排=0.015m²×0.26cm-8.75×10^-4m³=3.025×10^-3m³，
则液体质量为m=ρ_液V_液=1.6×10³kg/m³×3.025×10^-3m³=4.84kg．
故答案为：4.84．

点评：本题考查阿基米德原理的应用，重点是能分析物体A、B的受力情况，知道弹簧的伸长会引起液体的深度增加．