题目内容
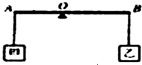如图所示，O为杠杆AB的支点，OA：0B=2：3．物块甲和乙分别在杠杆A、B两端，杠杆平衡．已知物块甲和乙体积相等，那么物块甲和乙的质量之比是分析：（1）甲、乙两物体的重力提供动力和阻力，因杠杆平衡，利用杠杆的平衡条件F1L1=F2L2即可求出质量之比．
（2）因甲、乙两物体体积相同，求出甲、乙两物体质量之比后结合密度的计算公式即可得出乙物体的密度．
（2）因甲、乙两物体体积相同，求出甲、乙两物体质量之比后结合密度的计算公式即可得出乙物体的密度．
解答：解：（1）因杠杆平衡，则F1L1=F2L2
m甲×g×OA=m乙×g×OB
2m甲=3m乙
m甲：m乙=3：2；
（2）m甲：m乙=3：2，V甲：V乙=1：1；
ρ甲：ρ乙=
：
=3：2=6.0×103Kg/m3：ρ乙
解得ρ乙=4.0×103Kg/m3=4000Kg/m3．
故答案为3：2；4000Kg/m3．
m甲×g×OA=m乙×g×OB
2m甲=3m乙
m甲：m乙=3：2；
（2）m甲：m乙=3：2，V甲：V乙=1：1；
ρ甲：ρ乙=
| m甲 |
| V甲 |
| m乙 |
| V乙 |
解得ρ乙=4.0×103Kg/m3=4000Kg/m3．
故答案为3：2；4000Kg/m3．
点评：本题考查的是杠杆平衡条件和密度计算的简单应用．
练习册系列答案
相关题目
如图所示，O为杠杆的支点，在杠杆的右端B点挂一重物．MN是以A为圆心的弧形导轨，绳的一端系在杠杆的A点，另一端E可以在弧形导轨上自由滑动．当绳的E端从导轨的一端N点向另一端M点滑动的过程中，杠杆始终水平，绳AE对杠杆拉力的变化情况（ ）
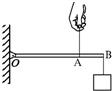如图所示，O为杠杆的支点，OA=40cm、OB=50cm，B点所挂物体重60N，要使杠杆在水平位置平衡，则在A点至少加一个方向为
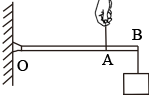如图所示，O为杠杆的支点，OA=40厘米，OB=50厘米，B点所挂物体重60牛，要使杠杆在水平位置平衡，则在A点至少加一个竖直向上
重12N的物体G挂在杠杆A点，如图所示．O为杠杆的支点，要使杠杆平衡，在B点要加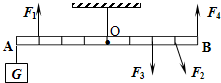
（2011?普陀区二模）如图所示，O为杠杆AB的支点，A端挂一重物G，图中能使杠杆在水平位置平衡的最小的拉力是（ ）