题目内容
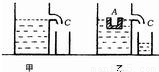
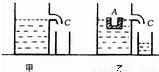
 一个竖直放置在水平桌面上的圆柱形容器,内装密度为ρ的液体,将挂在弹簧测力计下的金属块A浸没在该液体中(A与容器底未接触),金属块A静止时,弹簧测力计的示数为F,将木块B放入该液体中,静止后木块B露出液面的体积与其总体积之比为7:12;把金属块A放在木块B上,木块B刚好没入液体中(如图所示).若已知金属块A的体积与木块B的体积之比为13:24,则金属块的体积为
一个竖直放置在水平桌面上的圆柱形容器,内装密度为ρ的液体,将挂在弹簧测力计下的金属块A浸没在该液体中(A与容器底未接触),金属块A静止时,弹簧测力计的示数为F,将木块B放入该液体中,静止后木块B露出液面的体积与其总体积之比为7:12;把金属块A放在木块B上,木块B刚好没入液体中(如图所示).若已知金属块A的体积与木块B的体积之比为13:24,则金属块的体积为分析:先后分析将金属块A浸没在液体中、将木块B放入该液体中、把金属块A放在木块B上,利用称重法测浮力、漂浮条件、阿基米德原理列方程联立方程组求金属块A的体积.
解答:解:将金属块A浸没在液体中受到的浮力:
FA=GA-F=ρAvAg-F=ρvAg,-----------①
将木块B放入该液体中,木块漂浮,
FB=GB=mBg=ρBvBg=ρv排g,
∵静止后木块B露出液面的体积与其总体积之比为7:12,
∴v排:v=5:12,
∴FB=GB=ρv排g=
ρvBg,---------②
把金属块A放在木块B上,仍漂浮,
ρv排′g=ρvBg=GA+GB,------------③
①②③结合得出:
ρvBg=ρvAg+F+
ρvBg,即:
ρvBg=ρvAg+F;
∵vA:vB=13:24,
∴
ρ×
vAg=ρvAg+F,
∴vA=
.
故答案为:
.
FA=GA-F=ρAvAg-F=ρvAg,-----------①
将木块B放入该液体中,木块漂浮,
FB=GB=mBg=ρBvBg=ρv排g,
∵静止后木块B露出液面的体积与其总体积之比为7:12,
∴v排:v=5:12,
∴FB=GB=ρv排g=
| 5 |
| 12 |
把金属块A放在木块B上,仍漂浮,
ρv排′g=ρvBg=GA+GB,------------③
①②③结合得出:
ρvBg=ρvAg+F+
| 5 |
| 12 |
| 7 |
| 12 |
∵vA:vB=13:24,
∴
| 7 |
| 12 |
| 24 |
| 13 |
∴vA=
| 13F |
| ρg |
故答案为:
| 13F |
| ρg |
点评:本题考查了称重法测量金属块受到的浮力、漂浮条件、阿基米德原理,利用好两次的体积关系是本题的关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
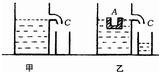 (2002?苏州)如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ,
(2002?苏州)如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ, 如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ,
如图甲所示,一圆柱形容器竖直放置在水平桌面上,其侧壁有一溢水口C,容器内的液面恰好与溢水口C齐平.先将一个由均匀材料制成的船形物A开口向上放入容器中,当船形物漂浮.在液面上(如图乙所示),从溢水口溢出液体的体积为V;然后使船形物A反转90°,当它浸没在液体中后容器内的液面下降了h(在船形物由漂浮到浸没的过程器内的液体未溢出).已知圆柱形容器的底面积为S,液体的密度为ρ,