��Ŀ����
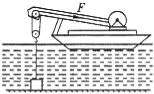
����Ŀ����ͼ��ʾ����ijˮ�ϴ��̴���һ����ȫ�ܱյ���������仺���ش��̳�ˮ������װ��ʾ��ͼ������ƽ���ں��ף��������H=30m���û���߳�L=1m�����估�ڲ����������G��=4.0��104N�������֣�ֻ��һ�������������������G����=1.0��104N���������غͻ���Ħ��������ˮ���ܵ��ĸ����������Ƿ��ˡ�ˮ���ȵ�Ӱ�죮����ˮ���ܶ���Ϊ��=1��103kg/m3��gȡ10N/kg�����ʣ�
��1��������̽������ϱ���Ļ�����ʱ���Ƕ��٣��������ں�ˮ�еĴ����ٶ�Ϊ��=1450m/s��
��2��Ҫ������Ӻ��״����ٵ����ϱ��潫¶��ˮ��Ĺ����У�����F���˶��ٹ���
��3��������Ӹ�¶��ˮ�浽��ȫ¶��ˮ��Ĺ������DZ����������ģ�������ڴ˹����У��������ܸ����ͻ������еЧ�ʵı仯�����
���𰸡���1��������̽������ϱ���Ļ�����ʱ����0.04s��
��2��Ҫ������Ӻ��״����ٵ����ϱ��潫¶��ˮ��Ĺ����У�����F����1.16��106J��
��3���ڴ˹����У��������ܸ�����С���������еЧ�ʵı��
��������
�����������1�����ŷ���ij������������侭������ֱ����Ž��գ������ߵ���2��H��L����·�̣������ٶȹ�ʽ��ʱ�䣻
��2����������������ó������ûˮ���ſ�ˮ����������ð�����ԭ���������ˮ���ܵ��ĸ�����������F=![]() ��G����+G����F�������������С�����������ˮ�е������߶ȣ�����W=Fh������F������
��G����+G����F�������������С�����������ˮ�е������߶ȣ�����W=Fh������F������
��3������Ӹ�¶��ˮ�浽��ȫ¶��ˮ��Ĺ����У������ܵ��ĸ�����С�������ܵ����������������������ù�������������䣬�ɴ˿�֪�����ֵĻ�еЧ�ʱ��
�⣺��1������֪�����ϱ������ˮ�棺
h=H��L=30m��1m=29m��
�����ߵ�·�̣�
s=2��H��L��=2��29m=58m��
������̽������ϱ���Ļ�����ʱ�䣺
t=![]() =
=![]() =0.04s��
=0.04s��
��2�������ſ�ˮ�������
v=��1m��3=1m3��
������ˮ���ܵ�ˮ�ĸ�����
F��=��ˮv��g=��ˮvg=1��103kg/m3��1m3��10N/kg=1��104N��
����F����
F=![]() ��G����+G����F����=
��G����+G����F����=![]() ��1.0��104N+4.0��104N��1.0��104N��=2��104N��
��1.0��104N+4.0��104N��1.0��104N��=2��104N��
�����ƶ��ľ��룺
s=2h=2��29m=58m��
����������
W=Fs=2��104N��58m=1.16��106J��
��3������Ӹ�¶��ˮ�浽��ȫ¶��ˮ��Ĺ����У������ſ�ˮ�������С�������ܵ��ĸ�����С�������ܵ����������������������ù�������������䣬�ɴ˿�֪�����ֵĻ�еЧ�ʱ��
�𣺣�1��������̽������ϱ���Ļ�����ʱ����0.04s��
��2��Ҫ������Ӻ��״����ٵ����ϱ��潫¶��ˮ��Ĺ����У�����F����1.16��106J��
��3���ڴ˹����У��������ܸ�����С���������еЧ�ʵı��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�