题目内容
【题目】起吊井底的一块石头．如果石头重力是500N，体积是0.02m3 ， 求：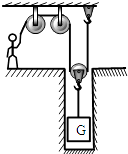 
（1）石头在水中受到的浮力？
（2）工人从水中匀速拉升石头时需拉力至少要多大？
（3）石头完全露出水面后，工人匀速拉升石头所用的拉力大小为260N，则此装置的机械效率是多少？
【答案】
（1）解：石头所受浮力：
F浮=ρ水V排g=ρ水Vg=1×103kg/m3×10N/kg×0.02m3=200N
答：石头在水中受到的浮力为200N
（2）解：工人从水中匀速拉升石头时，不计绳和动滑轮重、不计摩擦时需要的拉力最小，则所需拉力至少为：
F= 
（G﹣F浮）= （500N﹣200N）=150N
答：工人从水中匀速拉升石头时需拉力至少要150N
（3）解：由图知，n=2，设工人将石头升高了h米，拉力端移动距离s=2h，
则有用功：W有用=Gh，总功：W总=F拉s=F拉2h=2F拉h，
此装置的机械效率：
η= 
= 
= 
= 
= 
×100%≈96.2%
答：石头完全露出水面后，工人匀速拉升石头所用的拉力大小为260N，则此装置的机械效率是96.2%
【解析】由图知，使用的滑轮组承担物重的绳子股数n=2，拉力端移动距离s=2h．（1）知道石头的体积（在水中排开水的体积），利用阿基米德原理求石头所受浮力；（2）工人从水中匀速拉升石头时，不计绳和动滑轮重、不计摩擦时需要的拉力最小，此时拉力F= （G﹣F浮）；（3）设工人将石头升高了h米，拉力端移动距离s=2h，利用W=Gh求有用功，利用W=Fs求总功，再利用效率公式求此装置的机械效率．
【考点精析】解答此题的关键在于理解滑轮组绳子拉力的计算的相关知识，掌握1、根据题意确定重物和动滑轮的重力由几段绳承担，用n 表示．2、确定重物的上升距离，和拉力F 的绳端的移动距离；重物的上升距离为:h则拉力F 的绳端的移动距离就是：nh；3、看是否计动滑轮的重力．（绳重与摩擦一般情况都不计）当不计动滑轮重力时，拉力F = (1/n)G物 ；当计动滑轮重力时，拉力F = (1/n)（G物 + G轮），以及对阿基米德原理的理解，了解阿基米德原理：浸在液体中的物体受到向上的浮力，浮力的大小等于物体排开的液体所受的重力．这个规律叫做阿基米德原理，即 F浮= G排 =ρ液gv排．
