题目内容
 (2013?通州区二模)如图所示,某圆柱形容器内装有适量的水,底面积为20cm2.将物体B放入水中时,通过磅秤测得总质量为150g;使用一个杠杆提起物体B,发现当杠杆C端挂钩码A时,杠杆在
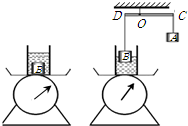
(2013?通州区二模)如图所示,某圆柱形容器内装有适量的水,底面积为20cm2.将物体B放入水中时,通过磅秤测得总质量为150g;使用一个杠杆提起物体B,发现当杠杆C端挂钩码A时,杠杆在水平位置恰好平衡,物体B刚好有一半体积露出水面.此时天平示数为50g,测得容器内液面下降了1cm.则物体B的密度为
3×103
3×103
kg/m3.(g取10N/kg)分析:由“通过磅秤测得总质量150g”可知其总重力,然后列出等式G容器+G水+GB=G1,同理列出等式G容器+G水+
F浮=G2,两式相减求得GB,再根据当B完全出水,液面将再下降1cm,圆柱形容器装有适量的水,底面积为20cm2,物体受到的浮力等于排开的水的重力,求出浮力,再根据液面下降1cm求出B的体积,最后利用ρ=
可求得此物体的密度.
| 1 |
| 2 |
| m |
| v |
解答:解:第一次通过磅秤测得总质量150g:则G容器+G水+GB=m1g=0.15kg×10N/kg=1.5N…①
B的体积:V=2△V=2S△h=2×20cm2×10-4×0.01m=4×10-5m3,
第二次此时磅秤示数为50g:则G容器+G水+
F浮=m2g=0.05×10N/kg=0.5N…②
由①-②得,GB-
F浮=1N…③,
B的一半体积浸入水中时比最先全部浸入水中时水面下降了1cm;
则圆柱形容器装有适量的水,底面积为20cm2,物体受到的浮力等于排开的水的重力,
即浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N
将F浮=0.4N代入③,解得GB=1.2N,则mB=
=
=0.12kg=120g.
则物体B的密度ρ=
=
=3g/cm3=3×103kg/m3.
故答案为:3×103.
B的体积:V=2△V=2S△h=2×20cm2×10-4×0.01m=4×10-5m3,
第二次此时磅秤示数为50g:则G容器+G水+
| 1 |
| 2 |
由①-②得,GB-
| 1 |
| 2 |
B的一半体积浸入水中时比最先全部浸入水中时水面下降了1cm;
则圆柱形容器装有适量的水,底面积为20cm2,物体受到的浮力等于排开的水的重力,
即浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×4×10-5m3=0.4N
将F浮=0.4N代入③,解得GB=1.2N,则mB=
| GB |
| g |
| 1.2N |
| 10N/kg |
则物体B的密度ρ=
| m |
| V |
| 120g |
| 40cm3 |
故答案为:3×103.
点评:解决此题的关键是利用公式和浮沉条件找等量关系,列等式,本题考查内容较多,计算量较大,在做题时力争能先进行细化逐个突破.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目