Question

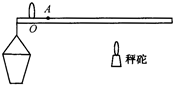（2009?海淀区二模）小明利用轻质硬棒（可视为杠杆）和透明塑料小桶等器材制作了如图所示的测量液体密度的秤：用细线做成提纽在O点将硬棒吊起，棒的一端悬挂塑料小桶（小桶中可装水或其他待测液体）．另外找一个重物作为秤砣，通过调节秤砣在硬棒上悬挂的位置，可使硬棒（杠杆）处于水平平衡．以下是小明测量某种待测液体密度时的实验步骤的一部分，请你将实验步骤补充完整．
（1）小桶内不加液体，手提O点处的提纽，移动秤砣位置，当秤砣置于A位置时使杠杆处于水平平衡．测量并记录此时O点到A点的距离l₀；
（2）将适量的水注入小桶中，在桶壁上标记水面位置．移动秤砣到某一位置，使杠杆再次处于水平平衡，测量并记录

此时O点到秤砣悬挂点的距离l₁

；
（3）将小桶内的水全部倒出，

再注入待测液体到达标记处，移动秤砣到另一位置，使杠杆再次水平平衡，测量并记录此时O点到秤砣悬挂点的距离l₂

；
（4）已知水的密度为ρ_水，利用上述测量出的物理量和已知量，写出计算待测液体密度ρ_液的表达式：ρ_液=

l2-l0

l1-l0

ρ_水

．

Answer 1

分析：根据杠杆平衡条件一定秤砣使杠杆平衡，并测出支点与秤砣间距离，保证液体体积和水的体积；
相掌握杠杆平衡条件：动力×动力臂=阻力×阻力臂列出没出平衡时的关系式，联立解答即可．

解答：解：设左端距O的距离为L，设秤砣的重力为G；
（1）小桶内不加液体，手提O点处的提纽，移动秤砣位置，当秤砣置于A位置时使杠杆处于水平平衡．测量并记录此时O点到A点的距离l₀；
根据杠杆平衡的条件可得：G_桶L=Gl₀----①
（2）将适量的水注入小桶中，在桶壁上标记水面位置．移动秤砣到某一位置，使杠杆再次处于水平平衡，测量并记录此时O点到秤砣悬挂点的距离l₁；
根据杠杆平衡的条件可得：G_桶L+ρ_水VgL=Gl₁----②
（3）将小桶内的水全部倒出，再注入待测液体到达标记处，移动秤砣到另一位置，使杠杆再次水平平衡，测量并记录此时O点到秤砣悬挂点的距离l₂；
根据杠杆平衡的条件可得：G_桶L+ρ_液VgL=Gl₂----③
联立①②③可得，ρ_液=

l2-l0

l1-l0

ρ_水．
故答案为：（2）此时O点到秤砣悬挂点的距离l₁；
（3）再注入待测液体到达标记处，移动秤砣到另一位置，使杠杆再次水平平衡，测量并记录此时O点到秤砣悬挂点的距离l₂；
（4）

l2-l0

l1-l0

ρ_水．

点评：本题是非常规题，难度较大，联系到杠杆平衡条件才能解答，关键是正确运用杠杆的平衡条件，同时在处理方程的时候也要注意技巧．