题目内容
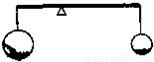
如图,轻质杠杆两端悬挂同种材料制成的大小不同的金属球时,杠杆平衡.把它们同时浸没在水中,杠杆仍然平衡,则下列说法可能正确的是( )
A.两球都是实心的
B.大球实心,小球空心
C.大球空心,小球实心
D.两球都空心,且空心部分体积相同
【答案】分析:判断两球是空心还是实心,其实就是判断两球的密度关系.那么要判断两球密度关系,我们需要根据题中条件,利用杠杆平衡条件和阿基米德原理列出两个等量关系式,然后再结合密度计算公式、重力计算公式进行推导.
解答:解:设大球的力臂为L大,小球的力臂为L小,大球的密度为ρ大,小球的密度为ρ小.
则两球在放入水中之前,根据杠杆的平衡条件可知:
G大L大=G小L小,
所以ρ大gV大L大=ρ小gV小L小,
则 =
= ;
;
当两球都浸没在水中时,根据杠杆的平衡条件可知:
(G大-F浮)L大=(G小-F浮)L小,
由阿基米德原理原理可得:
(ρ大gV大-ρ水gV大)L大=(ρ小gV小-ρ水gV小)L小,
则 =
= ;
;
综合前面两式得出: =
=
由此可得: =
= ,
,
所以(ρ大-ρ水)ρ小=(ρ小-ρ水)ρ大,
则ρ大ρ小-ρ水ρ小=ρ小ρ大-ρ水ρ大,那么ρ水ρ小=ρ水ρ大,所以ρ小=ρ大
A、当两球都是实心时,两球的密度才是相等的.
B、若大球实心,小球空心,则ρ大>ρ小.
C、若大球空心,小球实心,则ρ大<ρ小.
D、若两球实心,则ρ大=ρ小,即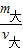 =
= .现在两球都是空心,且空心部分体积相同,则两球减小的质量都相同,设减小的质量都是m,而体积还是和原来相同,所以现在两个球的密度分别是ρ大′=
.现在两球都是空心,且空心部分体积相同,则两球减小的质量都相同,设减小的质量都是m,而体积还是和原来相同,所以现在两个球的密度分别是ρ大′= =
= -
-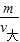 ,ρ小′=
,ρ小′=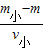 =
= -
-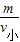 ,由于
,由于 =
= ,所以
,所以 -
- >
> -
- ,即ρ大′>ρ小′.
,即ρ大′>ρ小′.
故选 A.
点评:本题考查了杠杆的平衡原理以及浮力和密度知识的综合,难度比较大.解题中,要将两个球的重力、浮力通过公式展开,得出密度、g、体积和力臂的乘积,这样通过等式的建立,相等的量就可以消除,只剩下密度一个物理量.这类题要注意会运用公式进行物理量之间的推导和转化.
解答:解:设大球的力臂为L大,小球的力臂为L小,大球的密度为ρ大,小球的密度为ρ小.
则两球在放入水中之前,根据杠杆的平衡条件可知:
G大L大=G小L小,
所以ρ大gV大L大=ρ小gV小L小,
则
 =
= ;
;当两球都浸没在水中时,根据杠杆的平衡条件可知:
(G大-F浮)L大=(G小-F浮)L小,
由阿基米德原理原理可得:
(ρ大gV大-ρ水gV大)L大=(ρ小gV小-ρ水gV小)L小,
则
 =
= ;
;综合前面两式得出:
 =
=
由此可得:
 =
= ,
,所以(ρ大-ρ水)ρ小=(ρ小-ρ水)ρ大,
则ρ大ρ小-ρ水ρ小=ρ小ρ大-ρ水ρ大,那么ρ水ρ小=ρ水ρ大,所以ρ小=ρ大
A、当两球都是实心时,两球的密度才是相等的.
B、若大球实心,小球空心,则ρ大>ρ小.
C、若大球空心,小球实心,则ρ大<ρ小.
D、若两球实心,则ρ大=ρ小,即
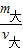 =
= .现在两球都是空心,且空心部分体积相同,则两球减小的质量都相同,设减小的质量都是m,而体积还是和原来相同,所以现在两个球的密度分别是ρ大′=
.现在两球都是空心,且空心部分体积相同,则两球减小的质量都相同,设减小的质量都是m,而体积还是和原来相同,所以现在两个球的密度分别是ρ大′= =
= -
-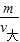 ,ρ小′=
,ρ小′=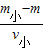 =
= -
-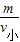 ,由于
,由于 =
= ,所以
,所以 -
- >
> -
- ,即ρ大′>ρ小′.
,即ρ大′>ρ小′.故选 A.
点评:本题考查了杠杆的平衡原理以及浮力和密度知识的综合,难度比较大.解题中,要将两个球的重力、浮力通过公式展开,得出密度、g、体积和力臂的乘积,这样通过等式的建立,相等的量就可以消除,只剩下密度一个物理量.这类题要注意会运用公式进行物理量之间的推导和转化.

练习册系列答案
相关题目
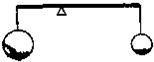 如图,轻质杠杆两端悬挂同种材料制成的大小不同的金属球时,杠杆平衡.把它们同时浸没在水中,杠杆仍然平衡,则下列说法可能正确的是( )
如图,轻质杠杆两端悬挂同种材料制成的大小不同的金属球时,杠杆平衡.把它们同时浸没在水中,杠杆仍然平衡,则下列说法可能正确的是( )| A、两球都是实心的 | B、大球实心,小球空心 | C、大球空心,小球实心 | D、两球都空心,且空心部分体积相同 |