题目内容
 (2009?青浦区二模)在图所示的电路中,电源电压为7.5V且不变,R1的电阻值为10欧,滑动变阻器R2上标有“20Ω 2A”字样,闭合电键S后,电压表的示数为2.5V.求:
(2009?青浦区二模)在图所示的电路中,电源电压为7.5V且不变,R1的电阻值为10欧,滑动变阻器R2上标有“20Ω 2A”字样,闭合电键S后,电压表的示数为2.5V.求:(1)滑动变阻器R2连入电路的阻值.
(2)电阻R1消耗的电功率P1.
(3)如果电路中电压表、电流表都使用小量程,为了不损坏电压表、电流表,保证电路正常工作,变阻器R2连入电路的阻值范围.
分析:由电路图可知,R1、R2串联,电压表测R2两端的电压,电流表测电路中的电流;
(1)根据串联电路的电压特点求出R1两端的电压,根据欧姆定律求出电路中的电流、求出滑动变阻器连入电路的阻值;
根据P=UI求出电阻R1消耗的电功率.
(2)电压表、电流表都使用小量程,根据保护电路的原则可知,电路中的最大电流为0.6A,根据欧姆定律求出R1两端的电压,根据串联电路的电压特点求出滑动变阻器两端的电压,根据欧姆定律求出滑动变阻器接入电路的最小值;当电压表的示数为3V时滑动变阻器接入电路的电阻最大,根据串联电路的电压特点求出R1两端的电压,根据欧姆定律求出电路中的电流,再根据欧姆定律求出滑动变阻器接入电路的最大阻值,从而可知变阻器R2连入电路的阻值范围.
(1)根据串联电路的电压特点求出R1两端的电压,根据欧姆定律求出电路中的电流、求出滑动变阻器连入电路的阻值;
根据P=UI求出电阻R1消耗的电功率.
(2)电压表、电流表都使用小量程,根据保护电路的原则可知,电路中的最大电流为0.6A,根据欧姆定律求出R1两端的电压,根据串联电路的电压特点求出滑动变阻器两端的电压,根据欧姆定律求出滑动变阻器接入电路的最小值;当电压表的示数为3V时滑动变阻器接入电路的电阻最大,根据串联电路的电压特点求出R1两端的电压,根据欧姆定律求出电路中的电流,再根据欧姆定律求出滑动变阻器接入电路的最大阻值,从而可知变阻器R2连入电路的阻值范围.
解答:解:(1)∵R1、R2串联
∴R1两端的电压U1=U-U2=7.5V-2.5V=5V,
电路中的电流I=I2=I1=
=
=0.5A,
滑动变阻器连入电路的阻值R2=
=
=5Ω;
(2)电阻R1消耗的电功率P1=U1I1=5V×0.5A=2.5W;
(3)当电路中的最大电流I最大=0.6A时,
电阻R1两端的电压U1′=I最大R1=0.6A×10Ω=6V,
滑动变阻器两端的电压U2′=U-U1′=7.5V-6V=1.5V,
滑动变阻器接入电路的最小值R2最小=
=
=2.5Ω;
当电压表的示数U2″=3V时,
电阻R1两端的电压U1″=U-U2″=7.5V-3V=4.5V,
电路的电流I″=I1″=
=
=0.45A,
动变阻器接入电路的最大值R2最大=
=
≈6.67Ω;
所以变阻器阻值范围为:2.5Ω~6.67Ω.
答:(1)滑动变阻器R2连入电路的阻值为5Ω;
(2)电阻R1消耗的电功率为2.5W;
(3)变阻器R2连入电路的阻值范围为2.5Ω~6.67Ω.
∴R1两端的电压U1=U-U2=7.5V-2.5V=5V,
电路中的电流I=I2=I1=
| U1 |
| R1 |
| 5V |
| 10Ω |
滑动变阻器连入电路的阻值R2=
| U2 |
| I2 |
| 2.5V |
| 0.5A |
(2)电阻R1消耗的电功率P1=U1I1=5V×0.5A=2.5W;
(3)当电路中的最大电流I最大=0.6A时,
电阻R1两端的电压U1′=I最大R1=0.6A×10Ω=6V,
滑动变阻器两端的电压U2′=U-U1′=7.5V-6V=1.5V,
滑动变阻器接入电路的最小值R2最小=
| ||
| I2 |
| 1.5V |
| 0.6A |
当电压表的示数U2″=3V时,
电阻R1两端的电压U1″=U-U2″=7.5V-3V=4.5V,
电路的电流I″=I1″=
| ||
| R1 |
| 4.5V |
| 10Ω |
动变阻器接入电路的最大值R2最大=
| ||
| I″ |
| 3V |
| 0.45A |
所以变阻器阻值范围为:2.5Ω~6.67Ω.
答:(1)滑动变阻器R2连入电路的阻值为5Ω;
(2)电阻R1消耗的电功率为2.5W;
(3)变阻器R2连入电路的阻值范围为2.5Ω~6.67Ω.
点评:对于电流表和电压表在同一个电路中,使其中一个满量程工作,要保证另一个的安全使用,不要顾此失彼,这是学生最容易出错的地方.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 (2009?青浦区二模)小明用力将弓拉开,如图所示,说明力能使物体发生
(2009?青浦区二模)小明用力将弓拉开,如图所示,说明力能使物体发生
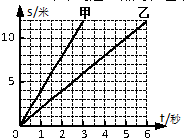 (2009?青浦区二模)M、N是同一直线上相距10米的两点,甲、乙两小车从M点出发向N点运动,它们运动的s-t图象如图所示,由图象可知( )
(2009?青浦区二模)M、N是同一直线上相距10米的两点,甲、乙两小车从M点出发向N点运动,它们运动的s-t图象如图所示,由图象可知( )