题目内容
 如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,所用动滑轮和筐的总重为20N.某次操作中,将重400N的泥土以速度v1=0.4m/s匀速提起一段高度后,稍作停歇,又以速度v2匀速将泥土提升一段高度,整个过程历时1min.在此过程中工人的拉力F所做的功随时间变化的图象可以简化为图乙所示.绳的质量忽略不计,g取10N/kg.求:
如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,所用动滑轮和筐的总重为20N.某次操作中,将重400N的泥土以速度v1=0.4m/s匀速提起一段高度后,稍作停歇,又以速度v2匀速将泥土提升一段高度,整个过程历时1min.在此过程中工人的拉力F所做的功随时间变化的图象可以简化为图乙所示.绳的质量忽略不计,g取10N/kg.求:(1)拉力F在后30s内做功的功率;
(2)利用该装置提升泥土的机械效率;
(3)在提起泥土上升3m的过程中,拉力F克服摩擦力做的功.(设在整个过程中,摩擦力大小保持不变)
分析:(1)由图象可知,拉力F在60s内做功是7200J,拉力F在后30s内做功为7200J-3600J,再根据P=
可求出拉力F在后30s内做功的功率.
(2)由图象可知,拉力F在20s内做功是3600J,W有用=G泥土h,再利用η=
×100%求出机械效率;
(3)由图甲可知,承担物重的绳子股数n=3,求出拉力端移动的速度,上面求出了拉力做功的功率,利用P=Fv求拉力大小;
再求出总功和有用功,因为W总=W有+W额,可求额外功,细绳的质量忽略不计,额外功有两部分:提升动滑轮、筐做功和克服摩擦做功,求出提升动滑轮做功,可求克服摩擦力做功.
| W |
| t |
(2)由图象可知,拉力F在20s内做功是3600J,W有用=G泥土h,再利用η=
| W有用 |
| W总 |
(3)由图甲可知,承担物重的绳子股数n=3,求出拉力端移动的速度,上面求出了拉力做功的功率,利用P=Fv求拉力大小;
再求出总功和有用功,因为W总=W有+W额,可求额外功,细绳的质量忽略不计,额外功有两部分:提升动滑轮、筐做功和克服摩擦做功,求出提升动滑轮做功,可求克服摩擦力做功.
解答:解:(1)拉力F在后30s内做功为W2=7200J-3600J=3600J,
则拉力F在后30s内做功的功率P=
=
=120W.
(2)拉力F在20s内做功W总=3600J,
W有用=G泥土h=400N×20s×0.4m/s=3200J,
该装置提升泥土的机械效率η=
×100%=
×100%≈88.9%.
(3)因为前20s匀速运动,所以P1=
=
=180W,
t2=
=
=7.5s,
=P1t2=180W×7.5s=1350J,
W物=G物h=400N×3m=1200J,
W筐=G筐h=20N×3m=60J,
Wf=
-W物-W筐=1350J-1200J-60J=90J.
答:(1)拉力F在后30s内做功的功率为120W.
(2)利用该装置提升泥土的机械效率为88.9%.
(3)在提起泥土上升3m的过程中,拉力F克服摩擦力做的功为90J.
则拉力F在后30s内做功的功率P=
| W |
| t |
| 3600J |
| 30s |
(2)拉力F在20s内做功W总=3600J,
W有用=G泥土h=400N×20s×0.4m/s=3200J,
该装置提升泥土的机械效率η=
| W有用 |
| W总 |
| 3200J |
| 3600J |
(3)因为前20s匀速运动,所以P1=
| W1 |
| t1 |
| 3600J |
| 20s |
t2=
| s |
| v |
| 3m |
| 0.4m/s |
| W | ′ 总 |
W物=G物h=400N×3m=1200J,
W筐=G筐h=20N×3m=60J,
Wf=
| W | ′ 总 |
答:(1)拉力F在后30s内做功的功率为120W.
(2)利用该装置提升泥土的机械效率为88.9%.
(3)在提起泥土上升3m的过程中,拉力F克服摩擦力做的功为90J.
点评:将物理规律或物理量的变化关系以图象、表格的形式呈现,体现了数学学科的基础性和工具性.迅速地从图象中提炼出有用信息是解决此类问题的关键.

练习册系列答案
相关题目
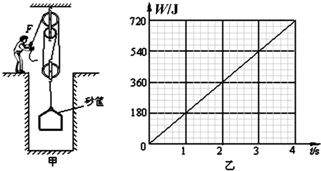
 如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,所用动滑轮和筐受到的总重力为20N.某次操作中,将重423N的泥土以0.4m/s的速度匀速提起,在工人提取泥土的全过程中,工人的拉力F所做的功随时间变化的图象如图乙所示.细绳的质量忽略不计,g取10N/kg.求:
如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,所用动滑轮和筐受到的总重力为20N.某次操作中,将重423N的泥土以0.4m/s的速度匀速提起,在工人提取泥土的全过程中,工人的拉力F所做的功随时间变化的图象如图乙所示.细绳的质量忽略不计,g取10N/kg.求: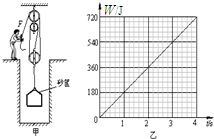 如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,某次操作中,将重
如图甲所示是工人利用滑轮组从竖直深井中提取泥土的情形,某次操作中,将重