题目内容
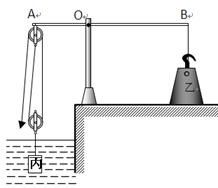
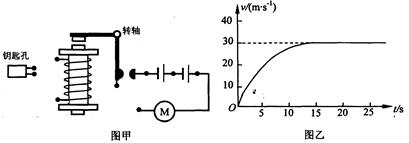
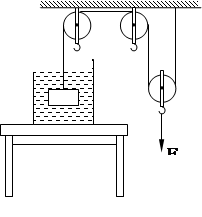
在图所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡。在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中。已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10cm2、高为12 cm,圆柱形容器的底面积为50cm2。若容器中的液体为水,在水深为20cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1:F2=3:4。若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18 cm,杠杆B端绳上的拉力为F3。取g=10N/kg,则


| A.圆柱形物体的密度为2 g/cm3 |
| B.作用在B端的拉力F3大小为1.52N |
| C.未知液体的密度为1.2 g/cm3 |
| D.未知液体对圆柱形容器底部的压强为1980Pa |
D
试题分析:A,设放水前后作用在A端绳子的拉力分别为F1′、F2′,圆柱体的体积为和密度分别为 V、ρ,则F1×OB=F1′×OA F2×OB=F4×OA ; ρ水Vg+3F1′=G=ρVg ; 1/3ρ水Vg+3F2′=G=ρVg 得圆柱体的密度ρ=3ρ水=3×1.0g/cm3=3g/cm3。B,F3=OA/OB×1/3(G-F浮)=2×1/3(2×103kg/m3×10N/kg×10cm2×12cm×10-6-1.1×103kg/m3×10N/kg×10cm2×10cm×10-6)=0.87N.C,水的体积是 V水=50cm2×20cm-10cm2×12cm=880cm3,未知液体的体积是 V=50cm2×18cm-10cm2×10cm=800cm3,由于质量相等,ρ水V水=ρV,故未知液体的密度 ρ液=ρ水V水 /V= 1.1g/cm3 ,D, P=ρ液gh=1.1×103kg/m3×10N/kg×0.18m=1980Pa,故答案选D
点评:本题难度较大,相当于一道计算题的量,同学们在遇到这样的题可以先跳过放到最后再做,关键是公式及其变形的灵活运用,对物体受力情况的分析,浮力密度体积等的计算要仔细。

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目

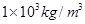 至
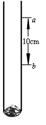
至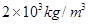 ,刻度线部分的长度ab为10cm,求这个密度计上分别写有
,刻度线部分的长度ab为10cm,求这个密度计上分别写有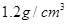 和
和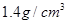 的两条刻度线之间的距离为 cm。
的两条刻度线之间的距离为 cm。