题目内容
一个身高为h(可看成是眼睛到地面的高度)的人面对竖直墙站立,身后有一棵高为H的树,人到墙和人到树的距离相等,在墙面上挂一面镜子,为了使人能从镜子中看到树的最高点,则平面镜的最高点离地面的最小高度是
- A.
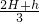
- B.
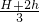
- C.
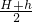
- D.

B
分析:设人离墙的距离是S,树离墙的距离为2S,对墙上的镜子作树的虚像,虚像距人的距离为3S,过人的眼睛A点作地面平行线,与树的虚像交于B点,
设树在镜中的虚像顶为C点,连接ABC组成一个直角三角形,利用相似三角形的性质求得DE,然后即可求得平面镜的最高点离地面的最小高度.
解答:如图所示:
(1)设人离墙的距离是S,树离墙的距离为2S,对墙上的镜子作树的虚像,虚像距人的距离为3S,过人的眼睛A点作地面平行线,与树的虚像交于B点,
(2)设树在镜中的虚像顶为C点,连接ABC组成一个直角三角形,AB与墙壁交于D,AC与墙壁交于E,底边BC=H-h,
因为树的虚像与墙壁平行,而人与墙的距离AD为S,人与虚像的距离AB为3S,由相似三角形定理,可得DE= ,所心需要的镜面上缘与地的距离为=
,所心需要的镜面上缘与地的距离为= +h=
+h=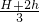 .
.
故选B.
点评:运用镜面对称性质,得到三角形相似,再由相似比三角形对应边成比例得出最后结果,运算过程比较简单,但画出图形,是个难点,此题对学生的要求比较高,要求学生应具备一定的空间想象能力.
分析:设人离墙的距离是S,树离墙的距离为2S,对墙上的镜子作树的虚像,虚像距人的距离为3S,过人的眼睛A点作地面平行线,与树的虚像交于B点,
设树在镜中的虚像顶为C点,连接ABC组成一个直角三角形,利用相似三角形的性质求得DE,然后即可求得平面镜的最高点离地面的最小高度.
解答:如图所示:

(1)设人离墙的距离是S,树离墙的距离为2S,对墙上的镜子作树的虚像,虚像距人的距离为3S,过人的眼睛A点作地面平行线,与树的虚像交于B点,
(2)设树在镜中的虚像顶为C点,连接ABC组成一个直角三角形,AB与墙壁交于D,AC与墙壁交于E,底边BC=H-h,
因为树的虚像与墙壁平行,而人与墙的距离AD为S,人与虚像的距离AB为3S,由相似三角形定理,可得DE=
 ,所心需要的镜面上缘与地的距离为=
,所心需要的镜面上缘与地的距离为= +h=
+h=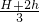 .
.故选B.
点评:运用镜面对称性质,得到三角形相似,再由相似比三角形对应边成比例得出最后结果,运算过程比较简单,但画出图形,是个难点,此题对学生的要求比较高,要求学生应具备一定的空间想象能力.

练习册系列答案
相关题目



