题目内容
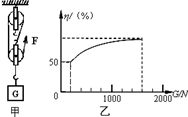
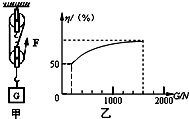 张强同学利用如图所示的滑轮组将货物运送到楼上,图中每个滑轮等重,不计绳子重和摩擦.如果所送货物重G从200N开始逐渐增加,直到绳子被拉断.每次均匀速拉动绳子,且提升高度都为10m.图乙记录了在整个过程中滑轮组的机械效率随货物的重力的增加而变化的图象.请根据有关信息完成以下问题:
张强同学利用如图所示的滑轮组将货物运送到楼上,图中每个滑轮等重,不计绳子重和摩擦.如果所送货物重G从200N开始逐渐增加,直到绳子被拉断.每次均匀速拉动绳子,且提升高度都为10m.图乙记录了在整个过程中滑轮组的机械效率随货物的重力的增加而变化的图象.请根据有关信息完成以下问题:(1)每个滑轮的重是多少?
(2)当货物重为1000N时,张强同学所做的总功为多少?
(3)绳子能承受的最大拉力是多少?
(4)当绳子的拉力最大时,滑轮组的机械效率是多少?
分析:(1)不计绳子重和摩擦,动滑轮不变,从乙图可知,取物重G=200N,知道此时的机械效率为50%,利用η=
=
=
=
计算动滑轮重.
(2)知道货物和动滑轮的重力,以及它们上升的高度,从而可利用公式W有用=Gh计算有用功,可利用公式W额外=G动h计算额外功,有用功和额外功的和为总功.
(3)从乙图象中可读出滑轮组能提升的最大物重,此时绳子承受的拉力最大.图甲的滑轮组由3段绳子承担物重,可利用公式F=
(G物+G动)求绳子能承受的最大拉力.
(4)知道提升的最大物重和货物上升的高度,可利用公式W有用=Gh计算有用功,最大动滑轮的重力和动滑轮上升的高度,可利用公式W额外=G动h计算额外功,再利用公式η=
=
求滑轮组的机械效率.
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
| G物h |
| G物h+G动h |
| G物 |
| G物+G动 |
(2)知道货物和动滑轮的重力,以及它们上升的高度,从而可利用公式W有用=Gh计算有用功,可利用公式W额外=G动h计算额外功,有用功和额外功的和为总功.
(3)从乙图象中可读出滑轮组能提升的最大物重,此时绳子承受的拉力最大.图甲的滑轮组由3段绳子承担物重,可利用公式F=
| 1 |
| n |
(4)知道提升的最大物重和货物上升的高度,可利用公式W有用=Gh计算有用功,最大动滑轮的重力和动滑轮上升的高度,可利用公式W额外=G动h计算额外功,再利用公式η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
解答:解:(1)由乙图可知:当G=200N时,η=50%,
∵η=
=
=
,
即:50%=
,
∴G动=200N.
(2)∵G物=1000N,G动=200N,h=10m,
∴有用功为:W有用=Gh=1000N×10m=10000J,
额外功为:W额外=G动h=200N×10m=2000J,
则总功为:W总=W有用+W额外=10000+:2000J=12000J.
(3)由乙图可知:当物重最大为G′=1600N时,绳子刚好被拉断,
而滑轮组由3段绳子吊着货物,
则绳子能承受的最大拉力:
F大=
(G′+G动)=
(1600N+200N)=600N.
(4)∵物重最大为G′=1600N,G动=200N,h=10m,
∴有用功为:W有用′=G′h=1600N×10m=16000J,
额外功为:W额外′=G动h=200N×10m=2000J,
则滑轮组的机械效率为:
η=
=
=
≈88.9%.
答:(1)每个滑轮的重是200N.
(2)当货物重为1000N时,张强同学所做的总功为12000J.
(3)绳子能承受的最大拉力是600N.
(4)当绳子的拉力最大时,滑轮组的机械效率是88.9%.
∵η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额 |
| G物 |
| G物+G动 |
即:50%=
| 200N |
| 200N+G动 |
∴G动=200N.
(2)∵G物=1000N,G动=200N,h=10m,
∴有用功为:W有用=Gh=1000N×10m=10000J,
额外功为:W额外=G动h=200N×10m=2000J,
则总功为:W总=W有用+W额外=10000+:2000J=12000J.
(3)由乙图可知:当物重最大为G′=1600N时,绳子刚好被拉断,
而滑轮组由3段绳子吊着货物,
则绳子能承受的最大拉力:
F大=
| 1 |
| 3 |
| 1 |
| 3 |
(4)∵物重最大为G′=1600N,G动=200N,h=10m,
∴有用功为:W有用′=G′h=1600N×10m=16000J,
额外功为:W额外′=G动h=200N×10m=2000J,
则滑轮组的机械效率为:
η=
| W有用′ |
| W总′ |
| W有用′ |
| W有用′+W额 |
| 16000J |
| 16000J+2000J |
答:(1)每个滑轮的重是200N.
(2)当货物重为1000N时,张强同学所做的总功为12000J.
(3)绳子能承受的最大拉力是600N.
(4)当绳子的拉力最大时,滑轮组的机械效率是88.9%.
点评:此题主要考查的是拉力、有用功、额外功、总功和滑轮组机械效率的计算方法,掌握机械效率、物重、动滑轮重之间的关系是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
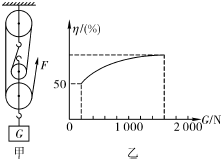 张强同学利用如图所示的滑轮组将货物运送到楼上,图中每个滑轮等重,不计绳子重和摩擦.如果所送货物重G从200N开始逐渐增加,直到绳子被拉断.每次均匀速拉动绳子,且提升同样的高度.图乙记录了在整个过程中滑轮组的机械效率随货物的重力的增加而变化的图象.请根据有关信息完成以下问题:
张强同学利用如图所示的滑轮组将货物运送到楼上,图中每个滑轮等重,不计绳子重和摩擦.如果所送货物重G从200N开始逐渐增加,直到绳子被拉断.每次均匀速拉动绳子,且提升同样的高度.图乙记录了在整个过程中滑轮组的机械效率随货物的重力的增加而变化的图象.请根据有关信息完成以下问题: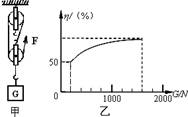
 滑轮的重是多少?
滑轮的重是多少?