题目内容
如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1´;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2´,OB:BC=1:2,杠杆和绳的质量忽略不计.求(1)F1´和F2´的比值;
(2)F的大小;
(3)如果要使物体D对地面的压强为零,杠杆在水平位置平衡时,需要在C点作用至少多大的力F´.

【答案】分析:(1)(2)对两种情况进行分析:
①由图知,在B点用力时,D对地面的压强,求出D的底面积,利用压强公式求D对地面的压力,而该压力等于D的重力减去杠杠的拉力,知道杠杠两边力的力臂关系,根据杠杠的平衡条件可得关于D的重GD和拉力F的方程;
②在C点用力时,同理得出关于D的重GD和拉力F的方程;
联立方程组求得F的大小、立方体D的重,也可求出F1´和F2´的比值;
(3)如果要使物体D对地面的压强为零,杠杠左边受力为D的重,知道杠杠两边力的力臂关系,根据杠杠的平衡条件求需要在C点的作用力.
解答:解:
因为OB:BC=1:2,所以OB:OC=1:3,又因为OA:OC=1:2,所以OA:OB=3:2,
在杠杆上B点施加力时,
∵p=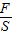 ,
,
∴D对地面的压力:
F压1=p1S=7000Pa×0.2m×0.2m=280N,
又∵D对桌面的压力等于D的重力减去杠杠的拉力,即F压1=GD-F1′,
∴F1′=GD-F压1=GD-280N,
∵杠杠平衡,
∴F1′×OA=F×OB,
∴F1′= F,----------①
F,----------①
即:GD-280N= F,-------------------②
F,-------------------②
在杠杆上C点施加力时,
∵p=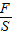 ,
,
∴D对地面的压力:
F压2=p2S=6000Pa×0.2m×0.2m=240N,
又∵D对桌面的压力等于D的重力减去杠杠的拉力,即F压2=GD-F2′,
∴F2′=GD-F压2=GD-240N,
∵杠杠平衡,
∴F2′×OA=F×OC,
∴F2′=2F,------------③
即:GD-240N=2F,------------------④
(1) 得:
得:
F1′:F2′= F:2F=1:3,
F:2F=1:3,
(2)④-②得:
40N=2F- F
F
∴F=30N;
(3)④代入②得:
GD-280N= (GD-240N)
(GD-240N)
解得:
GD=300N,
当物体D对地面的压强为零时,F3′=GD=300N,
∵杠杆在水平位置平衡
∴F3′×OA=F′×OC,
∴F′= F3′=
F3′= ×300N=150N.
×300N=150N.
答:(1)F1´和F2´的比值为1:3;
(2)F的大小为30N;
(3)如果要使物体D对地面的压强为零,杠杆在水平位置平衡时,需要在C点作用至少150N的力.
点评:本题考查了学生对压强公式、杠杠平衡条件、同一直线上力的合成的掌握和运用,能根据两种情况下的杠杠平衡条件得出的方程联立方程组求解是本题的关键.
①由图知,在B点用力时,D对地面的压强,求出D的底面积,利用压强公式求D对地面的压力,而该压力等于D的重力减去杠杠的拉力,知道杠杠两边力的力臂关系,根据杠杠的平衡条件可得关于D的重GD和拉力F的方程;
②在C点用力时,同理得出关于D的重GD和拉力F的方程;
联立方程组求得F的大小、立方体D的重,也可求出F1´和F2´的比值;
(3)如果要使物体D对地面的压强为零,杠杠左边受力为D的重,知道杠杠两边力的力臂关系,根据杠杠的平衡条件求需要在C点的作用力.
解答:解:
因为OB:BC=1:2,所以OB:OC=1:3,又因为OA:OC=1:2,所以OA:OB=3:2,
在杠杆上B点施加力时,
∵p=
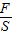 ,
,∴D对地面的压力:
F压1=p1S=7000Pa×0.2m×0.2m=280N,
又∵D对桌面的压力等于D的重力减去杠杠的拉力,即F压1=GD-F1′,
∴F1′=GD-F压1=GD-280N,
∵杠杠平衡,
∴F1′×OA=F×OB,
∴F1′=
 F,----------①
F,----------①即:GD-280N=
 F,-------------------②
F,-------------------②在杠杆上C点施加力时,
∵p=
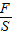 ,
,∴D对地面的压力:
F压2=p2S=6000Pa×0.2m×0.2m=240N,
又∵D对桌面的压力等于D的重力减去杠杠的拉力,即F压2=GD-F2′,
∴F2′=GD-F压2=GD-240N,
∵杠杠平衡,
∴F2′×OA=F×OC,
∴F2′=2F,------------③
即:GD-240N=2F,------------------④
(1)
 得:
得:F1′:F2′=
 F:2F=1:3,
F:2F=1:3,(2)④-②得:
40N=2F-
 F
F∴F=30N;
(3)④代入②得:
GD-280N=
 (GD-240N)
(GD-240N)解得:
GD=300N,
当物体D对地面的压强为零时,F3′=GD=300N,
∵杠杆在水平位置平衡
∴F3′×OA=F′×OC,
∴F′=
 F3′=
F3′= ×300N=150N.
×300N=150N.答:(1)F1´和F2´的比值为1:3;
(2)F的大小为30N;
(3)如果要使物体D对地面的压强为零,杠杆在水平位置平衡时,需要在C点作用至少150N的力.
点评:本题考查了学生对压强公式、杠杠平衡条件、同一直线上力的合成的掌握和运用,能根据两种情况下的杠杠平衡条件得出的方程联立方程组求解是本题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
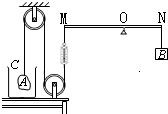 如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬挂着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置平衡.保持M点位置不动,向容器C中缓慢注水至A完全浸没在水中,测力计示数变为20N.托起容器C,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知判断错误的是( )
如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬挂着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置平衡.保持M点位置不动,向容器C中缓慢注水至A完全浸没在水中,测力计示数变为20N.托起容器C,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知判断错误的是( )| A、物体A的体积为2×103cm3 | ||
| B、物体A的密度为2×103kg/m3 | ||
C、物体B的悬挂点应向左移动的距离为杠杆长度的
| ||
| D、若将物体A从容器中取出,取出前后容器底部受水的压强的变化量为100Pa |
 (2008?海淀区二模)如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬吊着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置.现向容器C中缓慢注水,使A浸没,测力计示数变为20N.托起水杯,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知( )
(2008?海淀区二模)如图所示的装置,O为杠杆的支点,在杠杆上挂有重为60N的重物B,杠杆的左端通过细绳(绳的中间串一个弹簧测力计)跨过定滑轮悬吊着重物A处于静止状态,此时弹簧测力计的示数为40N,杠杆处于水平位置.现向容器C中缓慢注水,使A浸没,测力计示数变为20N.托起水杯,使A接触容器的底部,弹簧测力计的示数逐渐减为10N,同时移动物体B的悬挂点,使杠杆仍在水平位置平衡.若已知容器的底面积为200cm2,杠杆、弹簧测力计、细绳和滑轮的质量以及一切摩擦均可忽略不计,水的密度ρ=1.0×103kg/m3,取g=10N/kg.则根据以上数据可知( ) (2008?丰台区一模)如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.
(2008?丰台区一模)如图所示的装置,O为杠杆AC的支点,OA:OC=1:2,在杠杆的A点挂一边长为0.2m的立方体D,在杠杆上B点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p1为7000Pa,A点受到向下的拉力为F1?;在杠杆上C点作用竖直向下的拉力F,当杠杆在水平位置平衡时,物体D对地面的压强p2为6000Pa,A点受到向下的拉力为F2?,OB:BC=1:2,杠杆和绳的质量忽略不计.
