题目内容
假设雨点下落过程中受到空气的阻力与雨点(可看成球形)的横截面积S成正比,与下落速度v的平方成正比,即f阻=ksv2,其中k为比例常数.已知球的体积公式:V=
πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )
| 4 |
| 3 |
| A、1:2 | ||
B、1:
| ||
| C、1:4 | ||
| D、1:8 |
分析:已知雨点做匀速运动,阻力等于重力,还知道f阻=ksv2,以及球的体积公式,已知两个雨滴的半径之比,根据等式f阻=G可求这两个雨点的落地速度之比,G为雨点的重力.
解答:解:因为f阻=G=mg=ρVg=ksv2,还知道V=
πr3,s=πr2,整理可得ρg
πr3=kπr2v2,
所以v2=
,
则这两个雨点的落地速度平方之比为
=
=
=
,
所以
=
.
故选B.
| 4 |
| 3 |
| 4 |
| 3 |
所以v2=
ρg
| ||
| k |
则这两个雨点的落地速度平方之比为
| ||
|
ρg
| ||
ρg
|
| r1 |
| r2 |
| 1 |
| 2 |
所以
| v1 |
| v2 |
| 1 | ||
|
故选B.
点评:本题考查速度与物体的运动,关键是知道雨点做匀速运动,得出阻力等于重力,这是本题的转折点,也是本题的重点.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )
πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )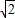
 πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )
πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )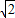
 πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )
πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )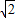
 πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )
πr3(r为半径),每个雨点的密度相同,且最终都做匀速运动.如果两个雨滴的半径之比为1:2则这两个雨点的落地速度之比为 ( )