题目内容
 (2000?长沙)如图所示,底面积为80cm2的容器中盛有深30cm的水.将一质量为540g的实心铝球投入水中.问:
(2000?长沙)如图所示,底面积为80cm2的容器中盛有深30cm的水.将一质量为540g的实心铝球投入水中.问:(1)铝球浸没在水中时受到的浮力是多大?
(2)投入铝球后,水对容器底部的压强增加了多少?
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为多大时绳子会拉断?(已知ρ铝=2.7×103kg/m3,取g=10N/kg).
分析:(1)先根据V=
求铝球的体积,铝球浸没在水中时排开水的体积和本身的体积相等,再根据F浮=ρgV排求出铝球浸没在水中受到的浮力;
(2)根据V=Sh求出铝球浸没时容器内水上升的高度,再根据p=ρgh求出容器底部压强的增加量;
(3)根据G=mg可知铝球的重力,绳恰好断掉时绳的拉力为4N,此时水中的铝块受到得浮力等于铝块重减去绳子的拉力,根据阿基米德原理可计算铝块在水中的体积,铝块露出水面的体积V露=V-V排.
| m |
| ρ |
(2)根据V=Sh求出铝球浸没时容器内水上升的高度,再根据p=ρgh求出容器底部压强的增加量;
(3)根据G=mg可知铝球的重力,绳恰好断掉时绳的拉力为4N,此时水中的铝块受到得浮力等于铝块重减去绳子的拉力,根据阿基米德原理可计算铝块在水中的体积,铝块露出水面的体积V露=V-V排.
解答:解:(1)根据ρ=
可得:
铝球的体积V铝=
=
=2×10-4m3,
根据阿基米德原理可得:
铝球浸没在水中时受到的浮力F浮=ρ水gV排=ρ水gV铝=1×103kg/m3×10N/kg×2×10-4m3=2N;
(2)设投入铝球后水面上升的高度为△H,则:
△H=
=
=
=0.025m,
水对容器底部增加的压强:
p=ρ水g△H=1×103kg/m3×10N/kg×0.025m=250Pa;
(3)设当铝球露出水面的体积为V露时,绳子会断,此时的浮力为F浮′,
则:F浮′=G-F拉,即ρ水gV排′=G-F拉
V排′=
=
=
=1.4×10-4m3,
铝球露出水面的体积:
V露=V-V排′=2×10-4m3-1.4×10-4m3=6×10-5m3.
答:(1)铝球浸没在水中时受到的浮力是2N;
(2)投入铝球后,水对容器底部的压强增加250Pa;
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为6×10-5m3时绳子会拉断.
| m |
| V |
铝球的体积V铝=
| m铝 |
| ρ铝 |
| 0.54kg |
| 2.7×103kg/m3 |
根据阿基米德原理可得:
铝球浸没在水中时受到的浮力F浮=ρ水gV排=ρ水gV铝=1×103kg/m3×10N/kg×2×10-4m3=2N;
(2)设投入铝球后水面上升的高度为△H,则:
△H=
| V排 |
| S |
| V铝 |
| S |
| 2×10-4m3 |
| 80×10-4m2 |
水对容器底部增加的压强:
p=ρ水g△H=1×103kg/m3×10N/kg×0.025m=250Pa;
(3)设当铝球露出水面的体积为V露时,绳子会断,此时的浮力为F浮′,
则:F浮′=G-F拉,即ρ水gV排′=G-F拉
V排′=
| G-F拉 |
| ρ水g |
| mg-F拉 |
| ρ水g |
| 0.54kg×10N/kg-4N |
| 1.0×103kg/m3×10N/kg |
铝球露出水面的体积:
V露=V-V排′=2×10-4m3-1.4×10-4m3=6×10-5m3.
答:(1)铝球浸没在水中时受到的浮力是2N;
(2)投入铝球后,水对容器底部的压强增加250Pa;
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为6×10-5m3时绳子会拉断.
点评:本题是一道力学综合题,要求灵活运用密度公式、重力公式、液体压强公式、阿基米德原理和力的合成,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
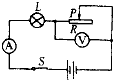 (2000?长沙)如图所示的电路中,电源电压保持不变.当滑动变阻器的滑片P向右滑动时,电流表和电压表的示数变化情况是( )
(2000?长沙)如图所示的电路中,电源电压保持不变.当滑动变阻器的滑片P向右滑动时,电流表和电压表的示数变化情况是( )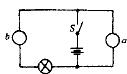 (2000?长沙)如图所示电路中,已知电表a、b的接法都是正确的,由图可知( )
(2000?长沙)如图所示电路中,已知电表a、b的接法都是正确的,由图可知( ) (2000?长沙)如图所示的曲线表示某晶体的熔化图象,其中
(2000?长沙)如图所示的曲线表示某晶体的熔化图象,其中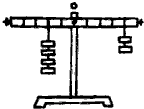 (2000?长沙)如图所示,刻度均匀的杠杆处于平衡状态,且每个钩码相同.若在支点两侧悬挂钩码处各再加挂一个钩码,那么杠杆
(2000?长沙)如图所示,刻度均匀的杠杆处于平衡状态,且每个钩码相同.若在支点两侧悬挂钩码处各再加挂一个钩码,那么杠杆