题目内容
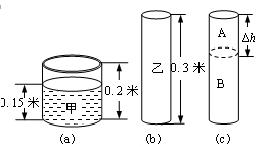
如图(a)所示,轻质薄壁圆柱形容器甲置于水平地面,底面积为2S,容器高0.2米,内盛0.15米深的水。
① 若容器的底面积为4×10-2米2,求容器中水的质量m。
② 求0.1米深处水的压强p。
③ 现有面积为S、密度为6r水圆柱体乙,如图(b)所示,在乙上方沿水平方向切去高为Δh的部分A(Δh<0.3米),如图(c)所示,将A放入容器甲中(A与甲底部没有密合),并将此时的容器置于剩余圆柱体B的上方中央。
(a)若要使水对容器底部的压强p水最大,求切去部分A高度的最小值Δh小。
(b)若要使水对容器底部的压强p水与地面受到的压强p地的比值最大,求切去部分A高度Δh的范围,并求比值p水/p地。
① 若容器的底面积为4×10-2米2,求容器中水的质量m。
② 求0.1米深处水的压强p。
③ 现有面积为S、密度为6r水圆柱体乙,如图(b)所示,在乙上方沿水平方向切去高为Δh的部分A(Δh<0.3米),如图(c)所示,将A放入容器甲中(A与甲底部没有密合),并将此时的容器置于剩余圆柱体B的上方中央。

(a)若要使水对容器底部的压强p水最大,求切去部分A高度的最小值Δh小。
(b)若要使水对容器底部的压强p水与地面受到的压强p地的比值最大,求切去部分A高度Δh的范围,并求比值p水/p地。
① m=ρV=103千克/米3×4×10-2米2×0.15米=6千克
②p=r gh=1×103千克/米3×9.8牛/千克×0.1米=980帕
③(a)2 S×(0.2m-0.15m)=S×Δh小 ,解得Δh小=0.1m。(b)p水=r gDh=0.2r g
p地=F/S=(G乙+G水—G溢)/S=2r g,p水/p地=0.2r g/2r g=1︰10,Dh≥0.2米
②p=r gh=1×103千克/米3×9.8牛/千克×0.1米=980帕
③(a)2 S×(0.2m-0.15m)=S×Δh小 ,解得Δh小=0.1m。(b)p水=r gDh=0.2r g
p地=F/S=(G乙+G水—G溢)/S=2r g,p水/p地=0.2r g/2r g=1︰10,Dh≥0.2米
试题分析:①由题意知容器中水的体积V= 4×10-2m2×0.15m=0.6×10-2m3,密度ρ=1.0×103kg/m3,水的质量m=ρV=1.0×103kg/m3×0.6×10-2m3=6kg。② 由题意知:水的密度ρ=1.0×103kg/m3,深度h=0.1m,g=9.8N/kg,则水产生的压强p=r gh=1.0×103kg/m3×9.8N/kg×0.1m=980Pa。③(a)要使水对容器底部的压强p水最大,切去部分A高度的最小,则A放入后,容器中的水刚满,由题意知2 S×(0.2m-0.15m)=S×Δh小 ,解得Δh小=0.1m。(b)要使水对容器底部的压强p水与地面受到的压强p地的比值最大,则使p水最大为p水=r gh最大=0.2r g,使p地最小,溢出的水最多,故切去部分A的高度范围为Dh≥0.2m,p地最小为p地=F/S=(G乙+G水—G溢)/S=(0.3×6ρSg+0.15×2ρSg-0.1×ρSg)=2r g,p水/p地=0.2r g/2r g=1︰10。

练习册系列答案
相关题目