题目内容
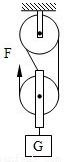
 如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求
如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求(1)拉力F的大小.
(2)所需时间.
分析:(1)由滑轮组可知,绳子的有效股数为3,根据s=nh可求绳子自由端移动的距离,根据W=Gh求出有用功,再根据效率公式求出总功,最后根据W=Fs的变形时求出拉力F的大小.
(2)已知拉力的功率,根据t=
求出所需时间.
(2)已知拉力的功率,根据t=
| W |
| P |
解答:解:(1)由图可知物体由3股绳子承担,
所以绳子自由端移动的距离s=nh=3×1m=3m,
滑轮组做的有用功W有=Gh=9×104N×1m=9×104J,
总功W总=
=
=1.125×105J,
拉力F的大小F=
=
=3.75×104N;
(2)所需时间:
t=
=
=5.625s.
答:(1)拉力F的大小为3.75×104N.
(2)所需时间为5.625s.
所以绳子自由端移动的距离s=nh=3×1m=3m,
滑轮组做的有用功W有=Gh=9×104N×1m=9×104J,
总功W总=
| W有 |
| η |
| 9×104J |
| 80% |
拉力F的大小F=
| W总 |
| s |
| 1.125×105J |
| 3m |
(2)所需时间:
t=
| W总 |
| P |
| 1.125×105J |
| 20000W |
答:(1)拉力F的大小为3.75×104N.
(2)所需时间为5.625s.
点评:本题考查了使用滑轮组拉力的计算、做功时间的计算,根据题图确定n的大小(直接从动滑轮上引出的绳子股数)是本题的突破口,利用好功的公式和机械效率是本题的关键.

练习册系列答案
相关题目
 如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求:
如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求: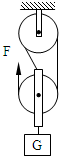 如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求:
如图所示,物重G=9×104N,滑轮组的机械效率为80%,滑轮组把重物匀速提高1m,拉力F做功的功率为20kW,求: