Question

【题目】如图所示，一轻质杠杆AB支在支架上，OA=20cm，G1为一边长为5cm的正方体，G2重为20N．当OC=10cm时，G1对地面的压强为2×104Pa．现用一水平拉力F使G2以2cm/s的速度向右匀速运动，则当G1对地面的压力为0时所经过的时间为（ ）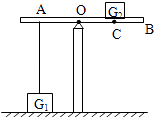
A.25s
B.30s
C.35s
D.40s

Answer 1

【答案】A
【解析】解：（1）G2在C点时，由杠杆平衡条件得： FA×OA=G2×OC，
即：FA×20cm=20N×10cm，
解得：
FA=10N；
物体与地面的接触面积：
S=5cm×5cm=25cm2=0.0025m2；
由p= 得：
物体G1对地面的压力：
F=pS=2×104Pa×0.0025cm2=50N，
地面对物体的支持力：
F′=F=50N，
G1受竖直向下的重力G1、地面的支持力F′、绳子的拉力FA作用，
物体静止，处于平衡状态，由平衡条件得：G1=FA+F′=10N+50N=60N；（2）当G1对地面的压力为0时，杠杆在A点的受到的拉力FA′=G1=60N，
设G2位于D点，由杠杆平衡条件得：FA′×OA=G2×OD，
即：60N×20cm=20N×OD，
解得：
OD=60cm，
物体G2的路程：
s=OD﹣OC=60cm﹣10cm=50cm，
由v= 得：物体G2的运动时间：
t= = =25s；
故选A．
【考点精析】根据题目的已知条件，利用杠杆的平衡分析法及其应用的相关知识可以得到问题的答案，需要掌握作关于杠杆题时的注意事项：（1）必须先找出并确定支点．（2）对力进行分析，从而确定动力和阻力（3）找出动力和阻力的作用线，确定动力臂和阻力臂．