题目内容
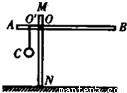
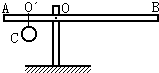在图中，杠杆AB是一根粗细均匀的轻质杠杆（重力不计），C是用细线挂在木杆O点上的小铁球，现杠杆恰好在水平位置平衡，且AO′=| 1 |
| 8 |
| 1 |
| 4 |
分析：先根据密度公式和重力公式求出铁球的重力，然后根据杠杆平衡的条件求出B处施加力的大小，并确定拉力的方向．
解答：解：查表可知，铁的密度为7.9×103kg/m3，则铁的质量：m铁=ρ铁v铁=7.9×103kg/m3×2×10-3m3=15.8kg，
铁的重力：G铁=mg=15.8kg×9.8N/kg=154.84N；
根据杠杆平衡的条件可得：
G铁×（OA-OA′）=FB×OB
154.84N×（
AB-
AB）=FB×
AB
FB=25.8N，方向竖直向上．
答：在B处至少应施加25.8N的拉力，方向竖直向上．
铁的重力：G铁=mg=15.8kg×9.8N/kg=154.84N；
根据杠杆平衡的条件可得：
G铁×（OA-OA′）=FB×OB
154.84N×（
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 4 |
FB=25.8N，方向竖直向上．
答：在B处至少应施加25.8N的拉力，方向竖直向上．
点评：本题考查学生对杠杆平衡条件的理解和掌握，正确找出力臂是解决此题的关键．
练习册系列答案
相关题目
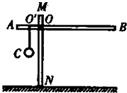在如图中，杠杆AB是一根粗细均匀的木杆，其质量为116g；C是用细线挂在木杆0′点上的铜铝合金球，其中含铝54g．现杠杆恰好在水平位置平衡．量得：AO′=
点上的铜铝合金球，其中含铝54g，现杠杆恰好在水平位置平衡，量得
＝AB/8，OA＝AB/4．求合金球C的密度为多少？(ρ铜＝8.9g/cm3，ρ铝＝2.7g/cm3)
在图中，杠杆AB是一根粗细均匀的轻质杠杆（重力不计），C是用细线挂在木杆O点上的小铁球，现杠杆恰好在水平位置平衡，且AO′=
AB、AO=
AB，如果C的体积为2×10-3m3．问：在B处至少应施加多大的拉力？拉力的方向？
AB，A0=
AB．问：合金球C的密度为多少？（铜的密度为ρ铜=8.9g/cm3，铝的密度ρ铝=2.7g/cm3）