题目内容
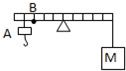（2002?长沙）如图，杠杆每小格的长度相等，质量不计，以O为支点，杠杆的右端挂有重物M，支点左边的A处挂钩码时，杠杆平衡，将重物M浸没在水中，钩码放在B处，杠杆又平衡，则重物与钩码的质量之比为4：5
4：5
，重物M的密度是4.0×103
4.0×103
kg/m3．分析：M未浸没水中，利用杠杆平衡条件，求出钩码和重物的质量关系；浸没后利用杠杆平衡条件求出右边对杠杆的拉力，再根据重物受力平衡求解
解答：解：（1）由题知，mgLOA=MgLOC，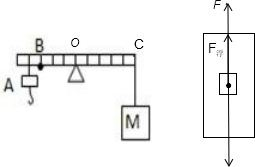
∴
=
=
（2）重物浸没前：mgLOA=MgLOC----------①，
重物浸没后：mgLOB=（Mg-F浮）LOC--------②，
②式比①式得：
=
= 1-
=
∴ρ物=4ρ水=4×103kg/m3
故答案为4：5，4×103kg/m3
∴
| M |
| m |
| LOA |
| LOC |
| 4 |
| 5 |
（2）重物浸没前：mgLOA=MgLOC----------①，
重物浸没后：mgLOB=（Mg-F浮）LOC--------②，
②式比①式得：
| LOB |
| LOA |
| Mg-F浮 |
| Mg |
| ρ水vg |
| ρ物vg |
| 3 |
| 4 |
∴ρ物=4ρ水=4×103kg/m3
故答案为4：5，4×103kg/m3
点评：本题用了4方面的知识：①重力公式G=mg=ρvg；②阿基米德原理；③物体受力平衡分析；④杠杆平衡条件
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
（2002?长沙）如图所示，将滑动变阻器连入电路，要求当滑片P向左移动时，电路中的电流增大，则滑动变阻器连入电路的接线柱应是（ ）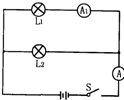
（2002?长沙）如图，已知电流表A1的读数为0.2安，电流表A的读数为0.3安，则通过灯L2的电流为