题目内容
如图所示,河两岸相互平行,相距为d,水流速度为v1,船相对水的速度为v2。船从岸边A点出发,船头始终垂直对岸,最终到达对岸B点。若保持v2的大小不变,适当改变v2的方向仍然从A点出发,发现航线与刚才恰好一致,但渡河时间变为原来的两倍。则可以判断( )
| A.v1:v2=2:1 |
| B.改变v2方向,可以使最短渡河时间为d/v2 |
C.改变v2方向,可以使最短渡河距离为 |
D.改变v2方向,可以使船到达对岸时向下游“漂移”的最短距离为 |
BD
解析试题分析:设AB与水平方向的夹角为θ,则当船头垂直于河岸时的合速度为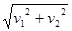 ,根据题意可得,当适当改变方向时的合速度为
,根据题意可得,当适当改变方向时的合速度为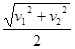 ,
,
则在三角形ACD中,cosθ=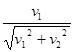 ,
,
在三角形AEC中,利用余弦定理得v22=(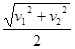 )2+v12-2
)2+v12-2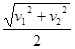 ×v1×
×v1×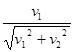 ,
,
解之得v1:v2=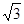 :1,故A是不对的;
:1,故A是不对的;
改变v2的方向,当v2的方向垂直于河岸时,船渡河时间最短,根据分速度的独立性原理,则最短时间为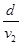 ,B是正确的;
,B是正确的;
改变v2的方向,为了使渡河的距离最短,则v2的方向应该与合速度的方向垂直,如图所示,则根据三角形相似的知识可知,三角形APQ相似于三角形AMN,即 ,故最短渡河距离AN=
,故最短渡河距离AN=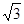 d,故C是不对的;
d,故C是不对的;
在直角三角形AMN中,由于AM=d,AN=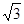 d,故MN=
d,故MN=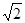 d,所以船到达对岸时向下游漂流的距离为
d,所以船到达对岸时向下游漂流的距离为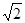 d,D
d,D
是正确的。
考点:运动的合成。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
如图所示,叠放在一起的物体A和B,在大小为F的恒力作用下沿水平面做匀速直线运动,则下列结论中正确的是( )
| A.甲、乙两图中A物体所受的摩擦力大小均为F |
| B.甲、乙两图中B物体受到地面对它的摩擦力均为F |
| C.甲图中物体A受到的摩擦力为0,物体B受到地面对它的摩擦力为F |
| D.乙图中物体A受到的摩擦力为F,物体B受到地面对它的摩擦力为F |
教室是同学们在校期间学习生活的主要场所。以下为教室内的有关数据,其中较为符合实际的是
| A.一只照明用日光灯的额定电流约为零点几安 |
| B.橡皮从课桌面掉到地面上所用的时间是五秒 |
| C.学生用课桌桌面的面积大约为二百平方厘米 |
| D.一间普通教室的内空气的质量约为三百千克 |
如图甲所示,某人在水平地面上用力推木箱,推力随时间变化的图像如图乙所示,木箱速度随时间变化的图像如图丙所示,以下对于这一过程的分析中正确的是 
| A.0—1s内木箱没有动是因为人对木箱的推力小于地面给木箱的摩擦力 |
| B.1s—2s内木箱受到的摩擦力大小为4N |
| C.2s—3s内人对木箱的推力做功为8J |
| D.如果3s后人停止用力,木箱将做匀速直线运动 |