题目内容
 如图,边长为0.5m的盛有水的立方体容器,放置在水平桌面上.水面上漂浮着密度均匀的长方体木块(木块在图中未画出),其表面与容器口相平.已知木块的密度为0.6×103kg/m3,边长分别为0.1m、0.2m、0.3m.
如图,边长为0.5m的盛有水的立方体容器,放置在水平桌面上.水面上漂浮着密度均匀的长方体木块(木块在图中未画出),其表面与容器口相平.已知木块的密度为0.6×103kg/m3,边长分别为0.1m、0.2m、0.3m.
求:(1)木块的质量.
(2)木块排开水的体积.
(3)水对容器底部产生的压强最大是多少?
已知,a=0.1m,b=0.2m,c=0.3m,ρ水=1.0×103kg/m3,ρ木=0.6×103kg/m3,h=0.5m
求:
(1)木块的质量m木;
(2)木块排开水的体积V排;
(3)水对容器底部产生的最大压强pmax.
解:(1)木块的体积:
V=abc=0.1m×0.2m×0.3m=0.006m3,
根据ρ=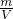 可得:
可得:
m木=ρ木V=0.6×103kg/m3×0.006m3=3.6kg,
(2)∵木块漂浮,
∴F浮=G木=m木g,
∵F浮=ρgV排,
∴ρ水gV排=m木g,
V排= =
= =3.6×10-3m3;
=3.6×10-3m3;
(3)当木块平放在水中时,液体的深度最大,水对容器底部产生的压强最大,
木块浸入水的深度:
h′=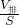 =
= =
= =0.06m,
=0.06m,
露出水面的高度:
h″=a-h′=0.1m-0.06m=0.04m,
此时液体的深度:
h水=h-h″=0.5m-0.04m=0.46m,
水对容器底部产生的最大压强:
pmax=ρ水gh水=1.0×103kg/m3×9.8N/kg×0.46m=4508Pa.
答:(1)木块的质量为3.6kg;
(2)木块排开水的体积3.6×10-3m3;
(3)水对容器底部产生的压强最大是4508Pa.
分析:(1)已知木块的边长可求体积,根据密度公式求出木块的质量;
(2)木块漂浮时受到的浮力和自身的重力相等,根据G=mg和阿基米德原理得出等式即可求出木块排开水的体积;
(3)当木块平方时,液体的深度最大,根据体积公式求出木块进入水的深度,再根据题意求出液体的深度,利用p=ρgh求出水对容器底部产生的最大压强.
点评:本题考查了密度公式和阿基米德原理、漂浮条件、液体压强公式的灵活应用,关键是根据题意得出木块平放在水中时,液体的深度最大水对容器底部产生的压强最大.
求:
(1)木块的质量m木;
(2)木块排开水的体积V排;
(3)水对容器底部产生的最大压强pmax.
解:(1)木块的体积:
V=abc=0.1m×0.2m×0.3m=0.006m3,
根据ρ=
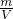 可得:
可得:m木=ρ木V=0.6×103kg/m3×0.006m3=3.6kg,
(2)∵木块漂浮,
∴F浮=G木=m木g,
∵F浮=ρgV排,
∴ρ水gV排=m木g,
V排=
 =
= =3.6×10-3m3;
=3.6×10-3m3;(3)当木块平放在水中时,液体的深度最大,水对容器底部产生的压强最大,
木块浸入水的深度:
h′=
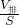 =
= =
= =0.06m,
=0.06m,露出水面的高度:
h″=a-h′=0.1m-0.06m=0.04m,
此时液体的深度:
h水=h-h″=0.5m-0.04m=0.46m,
水对容器底部产生的最大压强:
pmax=ρ水gh水=1.0×103kg/m3×9.8N/kg×0.46m=4508Pa.
答:(1)木块的质量为3.6kg;
(2)木块排开水的体积3.6×10-3m3;
(3)水对容器底部产生的压强最大是4508Pa.
分析:(1)已知木块的边长可求体积,根据密度公式求出木块的质量;
(2)木块漂浮时受到的浮力和自身的重力相等,根据G=mg和阿基米德原理得出等式即可求出木块排开水的体积;
(3)当木块平方时,液体的深度最大,根据体积公式求出木块进入水的深度,再根据题意求出液体的深度,利用p=ρgh求出水对容器底部产生的最大压强.
点评:本题考查了密度公式和阿基米德原理、漂浮条件、液体压强公式的灵活应用,关键是根据题意得出木块平放在水中时,液体的深度最大水对容器底部产生的压强最大.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
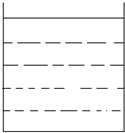 如图,边长为0.5m的盛有水的立方体容器,放置在水平桌面上.水面上漂浮着密度均匀的长方体木块(木块在图中未画出),其表面与容器口相平.已知木块的密度为0.6×103kg/m3,边长分别为0.1m、0.2m、0.3m.
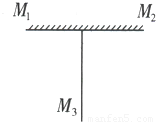
如图,边长为0.5m的盛有水的立方体容器,放置在水平桌面上.水面上漂浮着密度均匀的长方体木块(木块在图中未画出),其表面与容器口相平.已知木块的密度为0.6×103kg/m3,边长分别为0.1m、0.2m、0.3m.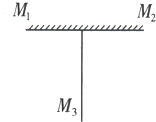 宇航员在月球上安装如图所示的装置,平面镜M1和M2在同一平面上,镜子M3有两个反射平面,这两个反射平面互相背对而合在一起,与M1垂直,M3的反射面朝向地球.在地球上向这个装置发射一束细激光.
宇航员在月球上安装如图所示的装置,平面镜M1和M2在同一平面上,镜子M3有两个反射平面,这两个反射平面互相背对而合在一起,与M1垂直,M3的反射面朝向地球.在地球上向这个装置发射一束细激光.