题目内容
如图所示立方体木块的质量为0.6kg,密度为0.6×103kg/m3,用细线系于底面积为500cm2的圆柱形容器的底部,木块浸没在水中静止,此时木块受到的浮力为 N,合力为 N:剪断细线后,当木块漂浮在水面上时,水位变化了 m,水对容器底的压强 (选填“增大”、“减小”、“不变”).
【答案】分析:(1)已知木块的质量和密度,可以得到其体积;因木块浸没在水中,所以V物=V排,再根据F浮=ρ液gV排即可求出木块浸没在水中时受到的浮力;由运动和力的关系知,物体处于静止状态,所受合力为零.
(2)由题意可知,剪断细线后,木块漂浮在水面上,则F浮=G=mg,知道了木块受到的浮力大小,根据阿基米德原理的变形公式算出此时木块在水中的V排;已知木块体积和排开水的体积,两者之差就是露出水面的体积;已知木块露出水面的体积和容器底面积,利用公式h=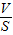 得到水位变化.
得到水位变化.
(3)液体压强公式是P=ρ液gh,判断压强变化只要分析液体密度和深度变化即可.
解答:解:
①木块的体积为V=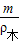 =
=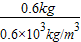 =1×10-3m3;
=1×10-3m3;
木块浸没在水中受到的浮力为F浮=ρ水gV排=1.0×103kg/m3×9.8N/kg×1×10-3m3=9.8N;
因为木块处于静止状态,所以受到的合力为0;
②剪断细线后,木块受到的浮力为F′浮=G=mg=0.6kg×9.8N/kg=5.88N
木块排开水的体积为V排=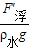 =
= =0.6×10-3m3;
=0.6×10-3m3;
木块露出水面的体积为△V=V-V排=1×10-3m3-0.6×10-3m3=0.4×10-3m3;
水面变化的高度为△h=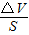 =
=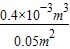 =8×10-3m;
=8×10-3m;
因为水的深度减小,所以由公式P=ρ液gh知,水对容器底的压强减小.
故答案为:9.8;0;8×10-3;减小.
点评:本题考查了阿基米德原理、物体的浮沉条件及其应用、液体压强公式的应用,其中剪断细线引起浮力、排开液体体积、水面高度、液体压强变化是分析的难点,突破的关键是对公式及其变形的熟练应用.
(2)由题意可知,剪断细线后,木块漂浮在水面上,则F浮=G=mg,知道了木块受到的浮力大小,根据阿基米德原理的变形公式算出此时木块在水中的V排;已知木块体积和排开水的体积,两者之差就是露出水面的体积;已知木块露出水面的体积和容器底面积,利用公式h=
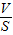 得到水位变化.
得到水位变化.(3)液体压强公式是P=ρ液gh,判断压强变化只要分析液体密度和深度变化即可.
解答:解:
①木块的体积为V=
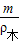 =
=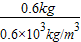 =1×10-3m3;
=1×10-3m3;木块浸没在水中受到的浮力为F浮=ρ水gV排=1.0×103kg/m3×9.8N/kg×1×10-3m3=9.8N;
因为木块处于静止状态,所以受到的合力为0;
②剪断细线后,木块受到的浮力为F′浮=G=mg=0.6kg×9.8N/kg=5.88N
木块排开水的体积为V排=
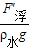 =
= =0.6×10-3m3;
=0.6×10-3m3;木块露出水面的体积为△V=V-V排=1×10-3m3-0.6×10-3m3=0.4×10-3m3;
水面变化的高度为△h=
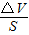 =
=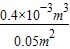 =8×10-3m;
=8×10-3m;因为水的深度减小,所以由公式P=ρ液gh知,水对容器底的压强减小.
故答案为:9.8;0;8×10-3;减小.
点评:本题考查了阿基米德原理、物体的浮沉条件及其应用、液体压强公式的应用,其中剪断细线引起浮力、排开液体体积、水面高度、液体压强变化是分析的难点,突破的关键是对公式及其变形的熟练应用.

练习册系列答案
相关题目
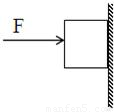
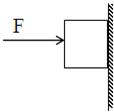 重2N,边长1dm的立方体木块,被3N的水平压力压在竖直墙上,如图所示,木块对墙的压力,压强分别是(g取10N/kg)( )
重2N,边长1dm的立方体木块,被3N的水平压力压在竖直墙上,如图所示,木块对墙的压力,压强分别是(g取10N/kg)( )| A、1N,100Pa | B、2N,300Pa | C、3N,300Pa | D、5N,500Pa |
 如图所示立方体木块的质量为0.6kg,密度为0.6×103kg/m3,用细线系于底面积为500cm2的圆柱形容器的底部,木块浸没在水中静止,此时木块受到的浮力为
如图所示立方体木块的质量为0.6kg,密度为0.6×103kg/m3,用细线系于底面积为500cm2的圆柱形容器的底部,木块浸没在水中静止,此时木块受到的浮力为 如图所示立方体木块的质量为0.6kg,密度为0.6×103kg/m3,用细线系于底面积为500cm2的圆柱形容器的底部,木块浸没在水中静止,此时木块受到的浮力为________N,合力为________N:剪断细线后,当木块漂浮在水面上时,水位变化了________m,水对容器底的压强________(选填“增大”、“减小”、“不变”).
如图所示立方体木块的质量为0.6kg,密度为0.6×103kg/m3,用细线系于底面积为500cm2的圆柱形容器的底部,木块浸没在水中静止,此时木块受到的浮力为________N,合力为________N:剪断细线后,当木块漂浮在水面上时,水位变化了________m,水对容器底的压强________(选填“增大”、“减小”、“不变”).