题目内容
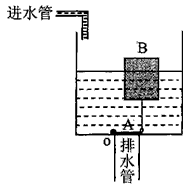
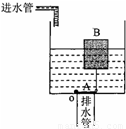
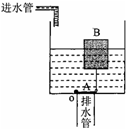 某学校课外科技小组的同学为学校的厕所设计了一个自动冲刷水箱.这种水箱能够把自来水管持续供给的较小流量的水储备到一定量后,自动开启放水阀,将水集中放出,这样就可以以较大的水流冲刷便池.如图所示,A是一面积为S1的圆形放水阀门,其质量和厚度均忽略不计,且恰好能将排水管口盖严.阀门的左端与排水管口的边缘相连并能绕垂直纸面的轴O向上转动,右端通过一很小的挂钩及连杆与浮子B相连,连杆的长度为h1,连杆质量和阀门转动受到的摩擦均不计.若将浮子B设计为一个质量为m、高为h2的空心圆柱体,它能将阀门拉起的最小横截面积S2是多少?
某学校课外科技小组的同学为学校的厕所设计了一个自动冲刷水箱.这种水箱能够把自来水管持续供给的较小流量的水储备到一定量后,自动开启放水阀,将水集中放出,这样就可以以较大的水流冲刷便池.如图所示,A是一面积为S1的圆形放水阀门,其质量和厚度均忽略不计,且恰好能将排水管口盖严.阀门的左端与排水管口的边缘相连并能绕垂直纸面的轴O向上转动,右端通过一很小的挂钩及连杆与浮子B相连,连杆的长度为h1,连杆质量和阀门转动受到的摩擦均不计.若将浮子B设计为一个质量为m、高为h2的空心圆柱体,它能将阀门拉起的最小横截面积S2是多少?
分析:先对物体进行受力分析,浮子静止时浮子受到向上浮力和向下的拉力和重力,浮子刚好将阀门拉起时,浮子和阀门连接在以O为支点的杠杆上,根据杠杆平衡条件列出等式,求出浮力的表达式,最后根据阿基米德原理求出它能将阀门拉起的最小横截面积.
解答:解:当浮子B处于静止状态时,F浮=T+mg,①
根据杠杆杠杆平衡原理,刚好将阀门打开时应满足Td=F水
=P水S1
,即T=P水
,②(d为阀门的直径),
①②联立可得:F浮=
+mg,
因为F浮=ρ水gV排,浮子刚好全部没入水中的面积就是最小面积,
所以ρ水gh2S2=mg+
,
整理可得:S2=
.
答:它能将阀门拉起的最小横截面积S2是
.
根据杠杆杠杆平衡原理,刚好将阀门打开时应满足Td=F水
| d |
| 2 |
| d |
| 2 |
| S1 |
| 2 |
①②联立可得:F浮=
| ρ水S1 |
| 2 |
因为F浮=ρ水gV排,浮子刚好全部没入水中的面积就是最小面积,
所以ρ水gh2S2=mg+
| ρ水g(h1+h2)S1 |
| 2 |
整理可得:S2=
m+
| ||
| h2ρ水 |
答:它能将阀门拉起的最小横截面积S2是
m+
| ||
| h2ρ水 |
点评:本题考查物体的受力分析和二力平衡的应用以及杠杆平衡条件的应用,难点是分析出物体静止时的受力和分析出要将阀门拉起,浮子刚好全部没入水中所需的最小浮力,即排开水的最小体积,因浮子高度是定值,进而求出浮子的最小底面积.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
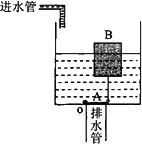
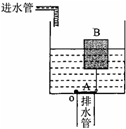 某学校课外科技小组的同学为学校的厕所设计了一个自动冲刷水箱.这种水箱能够把自来水管持续供给的较小流量的水储备到一定量后,自动开启放水阀,将水集中放出,这样就可以以较大的水流冲刷便池.如图所示,A是一面积为S1的圆形放水阀门,其质量和厚度均忽略不计,且恰好能将排水管口盖严.阀门的左端与排水管口的边缘相连并能绕垂直纸面的轴O向上转动,右端通过一很小的挂钩及连杆与浮子B相连,连杆的长度为h1,连杆质量和阀门转动受到的摩擦均不计.若将浮子B设计为一个质量为m、高为h2的空心圆柱体,它能将阀门拉起的最小横截面积S2是多少?
某学校课外科技小组的同学为学校的厕所设计了一个自动冲刷水箱.这种水箱能够把自来水管持续供给的较小流量的水储备到一定量后,自动开启放水阀,将水集中放出,这样就可以以较大的水流冲刷便池.如图所示,A是一面积为S1的圆形放水阀门,其质量和厚度均忽略不计,且恰好能将排水管口盖严.阀门的左端与排水管口的边缘相连并能绕垂直纸面的轴O向上转动,右端通过一很小的挂钩及连杆与浮子B相连,连杆的长度为h1,连杆质量和阀门转动受到的摩擦均不计.若将浮子B设计为一个质量为m、高为h2的空心圆柱体,它能将阀门拉起的最小横截面积S2是多少?