题目内容
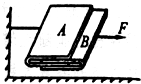
如图所示,有两本完全相同的书A、B,书重均为5牛,若将两本书分成若干份后,交叉地叠放在一起置于光滑桌面上,并将书A固定不动,用水平向右的力把书B抽出,现测得一组数据如下:
根据以上数据,试求:
(1)若将书分成32份,力F应为多大?
(2)该书的页数.
(3)如果我们把纸与纸接触面间的滑动摩擦力f和压力的比值叫做动摩擦因数μ,即μ=
且两本书的任意两张纸之间的动摩擦因素μ相等,则μ为多少?
| 实验次数 | 1 | 2 | 3 | 4 | … | n |
| 将书分成的份数 | 2 | 4 | 8 | 16 | … | 逐页交叉 |
| 力(F)的大小 | 4.5 | 10.5 | 22.5 | 46.5 | … | 190.5 |
(1)若将书分成32份,力F应为多大?
(2)该书的页数.
(3)如果我们把纸与纸接触面间的滑动摩擦力f和压力的比值叫做动摩擦因数μ,即μ=
| f |
| N |

(1)假设每本书的重量为G,纸张之间的摩擦系数为μ,那么当每本书被分为x份时,每一份的重力就为
;
根据摩擦力的定义,那么可以看到:
1部分对2部分的压力为1的重力,因此摩擦力为
,
2部分对3部分的压力为1、2的重力和,因此摩擦力为
,
3部分对4部分的压力为1、2、3的重力和,因此摩擦力为
,
4部分对5部分的压力为1、2、3、4的重力和,因此摩擦力为
,
…
以此类推
7部分对8部分的压力位1至7部分的重力和,因此摩擦力为
,
可以得到:右边被抽出的书收到的总摩擦力为F4=
=10.5N,
所以:μG=1.5N,
总的摩擦力:Fx=[1+2+3+…+(2x-1)]μG/x=(2x-1)μG,
即当x=32时,计算得到 F32=94.5N;
(2)当F=190.5N时,则:
(2x-1)μG=190.5N,
解得:x=64张,即128页;
(3)本书任意两张纸之间的滑动摩擦系数μ=
=0.3.
答:(1)若将书分成32份,力F应为94.5N;
(2)该书的页数为128页;
(3)本书任意两张纸之间的滑动摩擦系数μ为0.3.
| G |
| x |
根据摩擦力的定义,那么可以看到:
1部分对2部分的压力为1的重力,因此摩擦力为
| μG |
| 4 |
2部分对3部分的压力为1、2的重力和,因此摩擦力为
| 2μG |
| 4 |
3部分对4部分的压力为1、2、3的重力和,因此摩擦力为
| 3μG |
| 4 |
4部分对5部分的压力为1、2、3、4的重力和,因此摩擦力为
| 4μG |
| 4 |
…
以此类推
7部分对8部分的压力位1至7部分的重力和,因此摩擦力为
| 7μG |
| 4 |
可以得到:右边被抽出的书收到的总摩擦力为F4=
| (1+2+3+4+5+6+7)μG |
| 4 |
所以:μG=1.5N,
总的摩擦力:Fx=[1+2+3+…+(2x-1)]μG/x=(2x-1)μG,
即当x=32时,计算得到 F32=94.5N;
(2)当F=190.5N时,则:
(2x-1)μG=190.5N,
解得:x=64张,即128页;
(3)本书任意两张纸之间的滑动摩擦系数μ=
| 1.5N |
| 5N |
答:(1)若将书分成32份,力F应为94.5N;
(2)该书的页数为128页;
(3)本书任意两张纸之间的滑动摩擦系数μ为0.3.

练习册系列答案
相关题目