题目内容
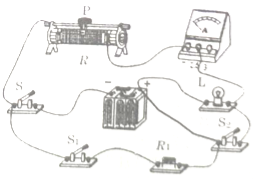
【题目】如图所示,电源电压保持不变,电阻R1为30Ω,小灯泡L标有“6V 3W”字样.闭合S,断开S1、S2,滑动变阻器滑片P移至最右端时,小灯泡L恰好正常发光;闭合S、S1、S2,滑片P移至最左端时,电路消耗的总功率为4.8W,忽略小灯泡电阻随温度的变化,求:
(1)电源电压及小灯泡L的电阻;
(2)滑动变阻器的最大阻值;
(3)闭合S,断开S1、S2,移动滑片P,使滑动变阻器的电功率为0.72W时,滑动变阻器连入电路的阻值.
【答案】(1)电源的电压为6V,小灯泡L的电阻12Ω;
(2)滑动变阻器的最大阻值10Ω;
(3)闭合S,断开S1、S2,移动滑片P,滑动变阻器连入阻值为8Ω
【解析】试题分析:(1)闭合S,断开S1、S2,滑动变阻器滑片P移至最右端时,小灯泡L恰好正常发光,此时是小灯泡的基本电路,故可判断电源电压,同时据灯泡正常发光,根据P=![]() 可计算小灯泡的电阻;
可计算小灯泡的电阻;
(2)闭合S、S1、S2,滑片P移至最左端时,R1与R并联,灯泡短路;由P=UI计算出总电流,利用欧姆定律可以计算出R1的电流,进而计算出滑动变阻器R 的电流,由欧姆定律可以计算R电阻.
(3)闭合S,断开S1、S2,移动滑片P,使滑动变阻器的电功率为0.72W时,灯泡与变阻器R串联,由串联电路特点、欧姆定律和P=I2R表示出变阻器的电功率,从而计算出变阻器连入的阻值.
解:
(1)由图知,闭合S,断开S1、S2,滑动变阻器滑片P移至最右端时,连入阻值为0,只有小灯泡的基本电路,小灯泡L恰好正常发光,
所以电源电压:U=U额=6V;
由P=![]() 可知,小灯泡的电阻是:
可知,小灯泡的电阻是:
RL=![]() =
=![]() =12Ω;
=12Ω;
(2)由图知,闭合S、S1、S2,滑片P移至最左端时,R1、R并联,小灯泡发生短路,
已知电路消耗的总功率为4.8W,由P=UI得:
I总=![]() =
=![]() =0.8A,
=0.8A,
由I=可得,通过R1的电流是:
I1=![]() =
=![]() =0.2A,
=0.2A,
由并联电路电流特点可得,通过滑动变阻器的电流是:
IR=I总﹣I1=0.8A﹣0.2A=0.6A,
所以滑动变阻器的最大电阻是:
R=![]() =
=![]() =10Ω;
=10Ω;
(3)闭合S,断开S1、S2,移动滑片P,使滑动变阻器的电功率为0.72W时,灯泡与变阻器R串联,
由串联电路特点和欧姆定律可得电路的电流为:
I=![]()
=![]() ,
,
由P=I2R可得变阻器的功率:
P滑=(![]() )2×R滑=0.72W,
)2×R滑=0.72W,
解得:R滑=8Ω,R滑=18Ω,
因为滑动变阻器最大值10Ω,故R滑=18Ω舍去.
答:(1)电源的电压为6V,小灯泡L的电阻12Ω;
(2)滑动变阻器的最大阻值10Ω;
(3)闭合S,断开S1、S2,移动滑片P,滑动变阻器连入阻值为8Ω.


