题目内容
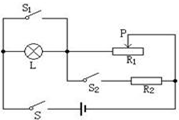 (2007?威海)如图所示,电源电压恒为24V,小灯泡标有“6V、3W”字样,定值电阻R2的阻值为24Ω,当S闭合,S1、S2都断开且滑片P移到滑动变阻器的中点时,灯L正常发光.
(2007?威海)如图所示,电源电压恒为24V,小灯泡标有“6V、3W”字样,定值电阻R2的阻值为24Ω,当S闭合,S1、S2都断开且滑片P移到滑动变阻器的中点时,灯L正常发光.(1)灯泡L的电阻是多少?
(2)滑动变阻器的最大阻值是多少?
(3)当S1、S2都闭合时,调节滑动变阻器,使整个电路消耗的总功率最小,这个最小值是多少?
分析:(1)由灯泡的铭牌信息可知灯泡的额定功率及额定电压,则由功率公式可求得灯泡的电阻;
(2)当S闭合,S1、S2都断开时,电路中灯泡及滑动变阻器串联,则由串联电路的欧姆定律可得出滑动变阻器两端的电压,由欧姆定律可求得滑动变阻器的接入电阻,由题意可知,最大阻值与接入电阻的关系,则可知最大阻值;
(3)当S1、S2都闭合时,R1与R2并联,因电源电压不变,则可知当电路电流最小时消耗的功率最小,即应使滑片滑到右端时,电路中消耗功率最小,则由并联电路的规律求得总电阻,由功率公式可求得最小功率.
(2)当S闭合,S1、S2都断开时,电路中灯泡及滑动变阻器串联,则由串联电路的欧姆定律可得出滑动变阻器两端的电压,由欧姆定律可求得滑动变阻器的接入电阻,由题意可知,最大阻值与接入电阻的关系,则可知最大阻值;
(3)当S1、S2都闭合时,R1与R2并联,因电源电压不变,则可知当电路电流最小时消耗的功率最小,即应使滑片滑到右端时,电路中消耗功率最小,则由并联电路的规律求得总电阻,由功率公式可求得最小功率.
解答:解:(1)由功率公式:P=
得:
灯泡的电阻:
R=
=
=12Ω;
(2)当S闭合,S1、S2都断开,L与R1串联,P位于中点L正常发光时
U1=U-U额=24V-6V=18V;
I=
=
=0.5A;
R1中=
=
=36Ω;
R1最大=2R1中=2×36Ω=72Ω;
(3)当S、S1、S2都闭合,R1、R2并联且滑片置于最右端时,电路消耗功率最小
R总=
=
=18Ω;
P最小=
=
=32W;
答:(1)灯泡的电阻为12Ω;(2)滑动变阻器的最大电阻为72Ω;(3)电路中消耗的最小功率为32W.
| U2 |
| R |
灯泡的电阻:
R=
| ||
| P额 |
| (6V)2 |
| 3W |
(2)当S闭合,S1、S2都断开,L与R1串联,P位于中点L正常发光时
U1=U-U额=24V-6V=18V;
I=
| P额 |
| U额 |
| 3W |
| 6V |
R1中=
| U1 |
| I |
| 18V |
| 0.5A |
R1最大=2R1中=2×36Ω=72Ω;
(3)当S、S1、S2都闭合,R1、R2并联且滑片置于最右端时,电路消耗功率最小
R总=
| R1R2 |
| R1+R2 |
| 24Ω×72Ω |
| 24Ω+72Ω |
P最小=
| U2 |
| R总 |
| (24V)2 |
| 18Ω |
答:(1)灯泡的电阻为12Ω;(2)滑动变阻器的最大电阻为72Ω;(3)电路中消耗的最小功率为32W.
点评:本题考查欧姆定律的应用及串并联电路的规律,要求学生具有较强的分析问题能力,分析电路图能力,并能将知识灵活应用.

练习册系列答案
相关题目
 (2007?威海)如图所示,悬吊的实心金属球缓慢浸没于倾斜的盛满水的大烧杯中,沉到底部,则从大烧杯溢出流入小烧杯中的水和此金属球的关系是( )
(2007?威海)如图所示,悬吊的实心金属球缓慢浸没于倾斜的盛满水的大烧杯中,沉到底部,则从大烧杯溢出流入小烧杯中的水和此金属球的关系是( ) (2007?威海)如图所示为研究磁场对通电导线作用的实验装置.当接通电源,有电流由a至b通过导线ab时,它将受到磁场力作用而向左运动,则( )
(2007?威海)如图所示为研究磁场对通电导线作用的实验装置.当接通电源,有电流由a至b通过导线ab时,它将受到磁场力作用而向左运动,则( )