题目内容
某人上午8:00从起点出发,途经三个不同的路段,先是上坡路,然后是较平直的路,最后是一段下坡路,三路段的长度均相同,在三个路段上的平均行驶速度之比为1:2:3,此人中午12:00正好到达终点.则上午10:00时他行进在( )A.上坡路段
B.平直路段
C.下坡路段
D.无法判断
【答案】分析:已知三个路段长度相同,已知平均速度之比,根据公式S=Vt可求所用时间之比,进一步求出每一段所用的时间,从而判断出上午10:00时他行进的路段.
解答:解:通过的路程相等:S=V1t1=V2t2=V3t3;又因为V1:V2:V3=1:2:3;所以时间之比为6:3:2;
全程所需时间为t=12:00-8:00=4h;
所以在上坡路上行驶的时间为t1=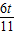 =
= ≈2h;
≈2h;
则上午10:00时他行进在上坡路上.
故选A.
点评:本题考查时间的计算,关键是公式及其变形的灵活运用,难点是判断出各段路所用的时间.
解答:解:通过的路程相等:S=V1t1=V2t2=V3t3;又因为V1:V2:V3=1:2:3;所以时间之比为6:3:2;
全程所需时间为t=12:00-8:00=4h;
所以在上坡路上行驶的时间为t1=
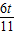 =
= ≈2h;
≈2h;则上午10:00时他行进在上坡路上.
故选A.
点评:本题考查时间的计算,关键是公式及其变形的灵活运用,难点是判断出各段路所用的时间.

练习册系列答案
相关题目