题目内容
【题目】如图所示,一质量为m的探空气球(包括其下方的吊篮)与吊篮中物体的质量之比为1:4,若气球所受总浮力始终保持30N不变,气球受到的空气阻力与速度成正比,即f=kv,此时气球以2m/s的速度竖直向下运动;若吊篮中的物体的质量减少一半,经过一段时间后,气球恰好以2m/s的速度竖直向上运动.求: 
(1)吊篮中物体的质量?
(2)若去掉吊篮中的所有物体,气球能达到的最大速度?(吊篮所受的浮力和空气阻力忽略不计,g=10N/kg)
【答案】
(1)解:气球质量为m,G球=10m,则物体重力为G物=40m
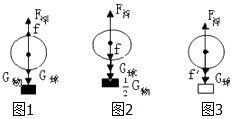
当气球匀速下降时,气球受力分析如图1所示,则由平衡条件得:
F浮+f=G球+G物﹣﹣﹣﹣﹣﹣①
当吊篮中物体的质量减少一半后,气球以同样匀速上升时,
气球受力分析如图2所示,则由平衡条件得:F浮=f+G球+G物﹣﹣﹣﹣﹣﹣②
把F浮=30N,G球=10m,G物=40m代入①②式,解得:f=7.5N m球=0.75kg;
则m物=4m球=4×0.75kg=3kg
(2)解:由f=kv1得,k= ![]() =
= ![]() =3.75;
=3.75;
当去掉吊篮中所有的物体时,气球上升,设最终匀速运动,速度最大为v,气球受力分析所图3所示,由平衡条件得:F浮=f′+G球;
则f′=F浮﹣G球=30N﹣0.75kg×10N/kg=22.5N;
由f′=kv 得v= ![]() =
= ![]() m/s=6m/s
m/s=6m/s
【解析】气球在空气中受到重力、阻力和浮力的作用,当匀速下降时,受到的力是平衡力; 气球在空气中受到重力、阻力和浮力的作用,当匀速上升时,受到的力是平衡力;
气球在上升和下降时,所受阻力的方向是不同的,阻力的方向总是与运动方向相反;
由平衡条件列方程求解.
【考点精析】掌握二力平衡条件的应用是解答本题的根本,需要知道二力平衡的条件是:作用在同一物体上的两个力大小相等,方向相反,且作用在同一直线上,即合力为零.(一物、二力、等大、反向、同直线).

 阅读快车系列答案
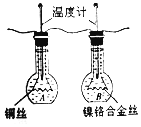
阅读快车系列答案【题目】小勇利用如图所示的实验装置“探究导体在磁场中运动时产生感应电流的条件”,他将实验中观察到的现象记录在如表中.
次数 | 开关 | 磁场方向 | 导体AB的运动方向 | 电流表指针的偏转方向 |
1 | 断开 | 上N下S | 向右运动 | 不偏移 |
2 | 闭合 | 上N下S | 向右运动 | 向左偏移 |
3 | 闭合 | 上N下S | 向左运动 | 向右偏移 |
4 | 闭合 | 上N下S | 向上运动 | 不偏移 |
5 | 闭合 | 上S下N | 向下运动 | 不偏移 |
6 | 闭合 | 上S下N | 向右运动 | 向右偏移 |
7 | 闭合 | 上S下N | 向左运动 | 向左偏移 |
(1)分析得出:电路中的部分导体在磁场里做切割磁感线运动时,导体中就会产生感应电流.
(2)比较实验2和3(或6和7)可知:在磁场方向一定时,感应电流的方向与有关.
(3)比较实验可知:在导体切割磁感线运动方向不变时,感应电流的方向与磁场方向有关.
(4)这个现象在生产和生活中的重要应用是 .
(5)针对这个实验,小勇进行了进一步的探究,他提出了“感应电流的大小可能与导体切割磁感线的运动速度有关”的猜想,于是他设计了如下的实验方案:①保持磁场强弱不变,让导体AB以(填“相同”或“不同”)的速度沿相同方向做切割磁感线运动,观察电流表指针偏转幅度大小.
②如果电流表指针偏转幅度不同,说明感应电流的大小与导体切割磁感线运动速度(填“有关”或“无关”).
【题目】在“探究实心圆柱体对地面的压强与哪些因素有关”的实验中,某中学一小组的同学们认为此压强跟圆柱体的密度ρ、高度h、圆柱体底面积S是有关的,但有怎样的关系看法不同,于是,在老师的帮助下,小组的同学们从实验室里挑选了由不同密度的合金材料制成、高度和横截面积不同、质量分布均匀的实心圆柱体做实验,测出实心圆柱体竖直放置时(如图所示)对水平桌面上海绵的压下深度,实验记录见下表。
序号 | 物体 | 底面积S/cm2 | 高度h/cm | 海绵被压下深度/cm |
1 | 合金甲圆柱体A | 10 | 5 | 0.5 |
2 | 合金甲圆柱体B | 10 | 10 | 1 |
3 | 合金甲圆柱体C | 20 | 10 | 1 |
4 | 合金乙圆柱体A | 10 | 5 | 1.5 |
5 | 合金乙圆柱体B | 10 | 10 | 3 |
6 | 合金乙圆柱体C | 20 | 10 | 3 |
(1)该小组同学是通过 来判断压强大小的。
(2)分析实验1、2或4、5可以得出:当圆柱体的材料密度相同时,实心圆柱体对水平地面的压强与圆柱体的 。
(3)分析 可以得出,当圆柱体的密度相同时,实心圆柱体对水平地面的压强与底面积无关。
(4)此探究过程用到的科学探究方法有 、 。
(5)实验结束之后,同学们在老师的指导下,以某一合金甲圆柱体为研究对象,推导它对海绵的压强大小的表达式(已知合金的密度为ρ,长方体铁块的高度为h,底面积为S)。表达式为 。
(6)上面推导出的表达式 (选填“能”或“不能”)应用于各类固体的压强的计算。