题目内容
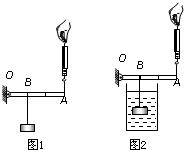 (2012?广西)如图,合金块重为6N,密度为8×103kg/m3,杠杆OA能绕着O点转动,OA=60cm,OB=20cm.不考虑测力计的重,g=10N/kg.问:
(2012?广西)如图,合金块重为6N,密度为8×103kg/m3,杠杆OA能绕着O点转动,OA=60cm,OB=20cm.不考虑测力计的重,g=10N/kg.问:(1)如图1,用杠杆把合金块匀速提升0.2m,提升时测力计的实际示数为2.25N,杠杆的机械效率是多少?
(2)在不计杠杆自重和摩擦的情况下,如果把合金块浸没在水中(如图2),杠杆静止时弹簧测力计的示数是多少?
分析:(1)由题知OA和OB大小、合金块上升高度,求出拉力端移动的距离,知道拉力大小和利用W=Fs求拉力做的总功;利用W=Gh求有用功;再利用效率公式求杠杆的机械效率.(1)由题知OA和OB大小、合金块上升高度,求出拉力端移动的距离,知道拉力大小和利用W=Fs求拉力做的总功;利用W=Gh求有用功;再利用效率公式求杠杆的机械效率.
(2)知道合金块重力,利用G=mg和ρ=
计算合金块的体积(浸没水中排开水的体积),利用阿基米德原理求合金块受到的浮力,进而求出杠杆B点受到的拉力,知道力臂关系,再利用杠杆平衡条件求杠杆静止时弹簧测力计的示数.
(2)知道合金块重力,利用G=mg和ρ=
| m |
| V |
解答:解:
(1)由题知,OA=60cm,OB=20cm,用杠杆把合金块匀速提升h=0.2m,拉力端移动的距离s=3h=3×0.2m=0.6m,
W有用=Gh=6N×0.2m=1.2J,
W总=Fs=2.25N×0.6m=1.35J,
η=
×100%=
≈88.9%;
(2)∵ρ=
,
∴合金块的体积:
V=
=
=
=
=7.5×10-3m3,
F浮=ρ水V排g=ρ水Vg=1×103kg/m3×7.5×10-3m3×10N/kg=0.75N,
杠杆受到的拉力:
FB=G-F浮=6N-0.75N=5.25N,
∵FALOA=FBLOB,
即:FA×60cm=5.25N×20cm,
∴FA=1.75N.
答:(1)杠杆的机械效率是88.9%;
(2)杠杆静止时弹簧测力计的示数是1.75N.
(1)由题知,OA=60cm,OB=20cm,用杠杆把合金块匀速提升h=0.2m,拉力端移动的距离s=3h=3×0.2m=0.6m,
W有用=Gh=6N×0.2m=1.2J,
W总=Fs=2.25N×0.6m=1.35J,
η=
| W有用 |
| W总 |
| 1.2J |
| 1.35J |
(2)∵ρ=
| m |
| V |
∴合金块的体积:
V=
| m |
| ρ |
| ||
| ρ |
| G |
| ρg |
| 6N |
| 8×103kg/m3×10N/kg |
F浮=ρ水V排g=ρ水Vg=1×103kg/m3×7.5×10-3m3×10N/kg=0.75N,
杠杆受到的拉力:
FB=G-F浮=6N-0.75N=5.25N,
∵FALOA=FBLOB,
即:FA×60cm=5.25N×20cm,
∴FA=1.75N.
答:(1)杠杆的机械效率是88.9%;
(2)杠杆静止时弹簧测力计的示数是1.75N.
点评:本题为力学综合题,考查了学生对机械效率公式、重力公式、密度公式、阿基米德原理、杠杆平衡条件的掌握和运用,知识点多、综合性强,属于难题,要求灵活运用所学知识!

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (2012?广西)如图所示,当试管内水沸腾时,软木塞突然被冲出来,其原因是试管内水蒸气对软木塞
(2012?广西)如图所示,当试管内水沸腾时,软木塞突然被冲出来,其原因是试管内水蒸气对软木塞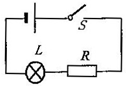 (2012?广西)如图所示,标有“5V 5W”字样的小灯泡L与电阻R串联在电路中,电源电压为8V.当开关S闭合时,小灯泡恰好正常发光,则小灯泡的电阻为
(2012?广西)如图所示,标有“5V 5W”字样的小灯泡L与电阻R串联在电路中,电源电压为8V.当开关S闭合时,小灯泡恰好正常发光,则小灯泡的电阻为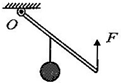 (2012?广西)如图所示,请画出力F的力臂L.
(2012?广西)如图所示,请画出力F的力臂L.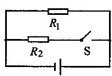 (2012?广西)如图所示,电源电压为3V,R2=10Ω.开关闭合时,通过R1的电流为0.2A.求:
(2012?广西)如图所示,电源电压为3V,R2=10Ω.开关闭合时,通过R1的电流为0.2A.求: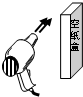 (2012?广西)如图所示,课堂上物理老师把一个轻的空纸盒竖立在讲台上,让电吹风的风从它左边侧面吹过(不吹到盒子),可以看到盒子将向
(2012?广西)如图所示,课堂上物理老师把一个轻的空纸盒竖立在讲台上,让电吹风的风从它左边侧面吹过(不吹到盒子),可以看到盒子将向