题目内容
【题目】（6分）如图所示，一根质量分布均匀的木棒，质量为m,长度为L，竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置（转轴处摩擦不计）。问：
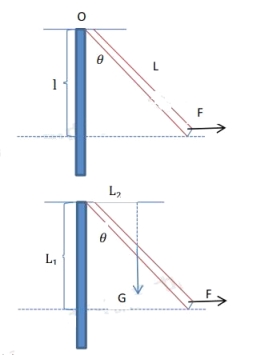
（1）在答题纸上画出θ=60°时拉力F的力臂L1，并计算力臂的大小。
（2）木棒的重力作用点在其长度二分之一处，随拉开角度θ的增加，拉力F将如何变化？
并推导拉力F与角度θ的关系式。
【答案】（1）1/2L （2）F=1/2mgtanθ 当0＜θ＜90°时，tanθ随θ的增大而增大。
【解析】
试题分析：（1）θ=60°时拉力F的力臂L1 =Lcosθ=Lcos60°=L/2 ；
（2）由杠杆平衡得： FL1=GL2，L2= Lsinθ/2
即FLcosθ=G Lsinθ/2
∴ F= mgtanθ/2
当0＜θ＜90°时，tanθ随θ的增大而增大，拉力F也随之增大。
【考点定向】杠杆平衡条件的应用
练习册系列答案
相关题目
【题目】（6分）小明在研究“影响滑动摩擦力大小的因素”时，提出了如下猜想：
猜想一：滑动摩擦力的大小与接触面所受的压力有关；
猜想二：滑动摩擦力的大小与接触面的粗糙程度有关。
为了验证猜想，准备了如下实验器材：一个带挂钩的木块（重6N）、两个砝码（每个重5N）、一块长木板和一个弹簧测力计。所用实验装置如图所示。
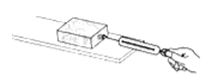
在验证猜想一时，用弹簧测力计水平拉动木块，使它沿水平木板做匀速直线运动，读取弹簧测力计的示数；在木块上分别放置一个和两个砝码，按上述操作再做两次实验，得到的实验数据如下表所示。
实验次数 | 压力/N | 测力计的示数/N | 滑动摩擦力/N |
1 | 6 | 1.8 | |
2 | 11 | 3.3 | |
3 | 16 | 4.8 |
（1）请将表中空格部分填写完整；
（2）结合实验过程分析表中数据，得出的结论是 ；
（3）为了验证猜想二，还需增加的实验器材： 。
