题目内容
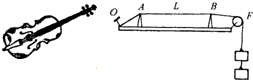
弦乐器小提琴是由两端固定的琴弦产生振动而发音的,如图所示.为了研究同一根琴弦振动频率与哪些因素有关,可利用如图所示的实验装置.一块厚木板上有AB两个楔支撑着琴弦,其中A楔固定,B楔可沿木板移动来改变琴弦振动部分的长度L.将琴弦的末端固定在木板O点,另一端通过滑轮接上砝码以提供一定拉力F,轻轻拨动琴弦,在AB间产生振动.

(1)先保持拉力F为150N不变,改变AB的距离L(即改变琴弦长度),测出不同长度时琴弦振动的频率,记录结果如表1所示.从表1数据可判断在拉力F不变时,琴弦振动的频率f与弦长L的关系式为________.
表 1
| 琴弦长度L (m) | 1.50 | 1.00 | 0.75 | 0.50 | 0.40 |
| 振动频率f (Hz) | 100 | 150 | 200 | 300 | 375 |
表 2
| 拉力大小F (N) | 360 | 300 | 240 | 180 | 120 |
| 振动频率f (Hz) | 290 | 265 | 237 | 205 | 168 |
| 振动频率的平方f 2(Hz2) | 84100 | 70225 | 56169 | 42025 | 28224 |
解:(1)通过表格数据可以看出弦越长,频率越低,我们可以看两者之间是否存在反比关系,即F=fL;
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,
我们现在表格中写出对应的拉力大小平方根 的数据,
的数据,
可以作出f- 图象,如果图形是过原点的直线,那么可以说明f与
图象,如果图形是过原点的直线,那么可以说明f与 成正比,即得频率f与拉力F的平方根成正比.
成正比,即得频率f与拉力F的平方根成正比.
根据以上可以得出频率f=k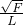 ,
,
(3)据实际情况可知,不同种类的小提琴琴弦,除了长度L和拉力F 以外,还与琴弦材料的种类、琴弦的粗细等因素有关.
故答案为:(1)F=fL;(2)f=k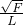 ;(3)琴弦材料的种类;琴弦的粗细.
;(3)琴弦材料的种类;琴弦的粗细.
分析:(1)通过表格数据分析频率和弦长之间的关系.弦越长,频率越低,看两者之间是否存在反比关系,进而可得出关系公式.
(2)通过表格数据分析频率和拉力的关系.拉力越大,频率越高,我们可以去作出f-F图象,或f- 图象,如果图形是过原点的直线,我们可以说明两个变量是成正比关系.
图象,如果图形是过原点的直线,我们可以说明两个变量是成正比关系.
(3)据实际情况进行判断即可.
点评:一个物理量受多个因素影响时,探究其中一个因素和物理量的关系时,控制其他因素不变,这种方法是控制变量法,在物理探究实验中经常用到,一定要掌握.从数据中分析两个量之间的关系时,是本题的一个难点.
(2)保持琴弦长度为0.80m不变,改变拉力,测出不同拉力时琴弦振动的频率,
我们现在表格中写出对应的拉力大小平方根
 的数据,
的数据,拉力大小平方根 / /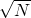 | 19.0 | 17.3 | 15.5 | 13.4 | 11.0 |
| 振动频率f/Hz | 290 | 265 | 237 | 205 | 168 |
 图象,如果图形是过原点的直线,那么可以说明f与
图象,如果图形是过原点的直线,那么可以说明f与 成正比,即得频率f与拉力F的平方根成正比.
成正比,即得频率f与拉力F的平方根成正比.根据以上可以得出频率f=k
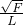 ,
,(3)据实际情况可知,不同种类的小提琴琴弦,除了长度L和拉力F 以外,还与琴弦材料的种类、琴弦的粗细等因素有关.
故答案为:(1)F=fL;(2)f=k
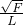 ;(3)琴弦材料的种类;琴弦的粗细.
;(3)琴弦材料的种类;琴弦的粗细.分析:(1)通过表格数据分析频率和弦长之间的关系.弦越长,频率越低,看两者之间是否存在反比关系,进而可得出关系公式.
(2)通过表格数据分析频率和拉力的关系.拉力越大,频率越高,我们可以去作出f-F图象,或f-
 图象,如果图形是过原点的直线,我们可以说明两个变量是成正比关系.
图象,如果图形是过原点的直线,我们可以说明两个变量是成正比关系.(3)据实际情况进行判断即可.
点评:一个物理量受多个因素影响时,探究其中一个因素和物理量的关系时,控制其他因素不变,这种方法是控制变量法,在物理探究实验中经常用到,一定要掌握.从数据中分析两个量之间的关系时,是本题的一个难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目