题目内容
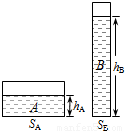
如图所示,两柱形容器内装有A、B两种体积相同的液体,A液体深度是B 液体深度的2倍,两种液体对容器底部的压强相同.若将甲、乙两物块分别投入A、B两液体中,液体均未溢出,且甲物块在A中悬浮,乙物块密度是甲物块的3倍,乙物块所受浮力等于甲物块重的一半.则这时两容器底部所受液体的压强分别增加为pa和pb,则pa= pb.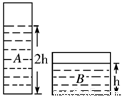
【答案】分析:本题要求两容器底部所受液体的压强增加之比,根据p=ρgh可知,应先求两种液体密度之比与液面深度变化之比;
(1)由物体放入之前压强相等,液体体积相等,得出两种液体的密度之比,两容器底面积之比;
(2)放入物体后:根据甲悬浮、乙物块所受浮力等于甲物块重的一半,得出甲乙两物体排开液体的体积之比;
(3)根据V排之比与底面积之比求得液面深度变化之比;
(4)最后由: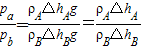 求得压强之比.
求得压强之比.
解答:解:
(1)物体放入之前:pA=pB,hA=2hB;
即:ρAghA=ρBgh B;
所以: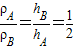 ;--①
;--①
(2)物体放入之后,甲悬浮;
所以:V甲=V甲排;甲受到的浮力F甲=G甲;ρ甲=ρA;
由题知:乙物块所受浮力等于甲物块重力的一半;
所以:F乙=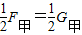 ;
;
即:ρBV乙排g= ρAV甲排g;
ρAV甲排g;
 ;
;
(3)由题知:放入物体之前,两柱形容器内装有A、B两种体积相同的液体;
所以:VA=VB;sAhA=sBhB;
即: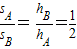 ;
;
(4)根据排开液体体积的关系求深度变化的关系;
 ;
;
即: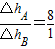 ;--②
;--②
(5)根据上面①②两式得出压强变化之比:
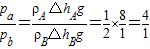 ;
;
故答案为:4.
点评:此题考查了液体压强的计算,难度较大,关键是找到比较压强变化的方法:即压强变化跟液体密度与深度变化的关系;公式多,计算复杂,这样难度的问题在近几年的中考中几乎不见了.
(1)由物体放入之前压强相等,液体体积相等,得出两种液体的密度之比,两容器底面积之比;
(2)放入物体后:根据甲悬浮、乙物块所受浮力等于甲物块重的一半,得出甲乙两物体排开液体的体积之比;
(3)根据V排之比与底面积之比求得液面深度变化之比;
(4)最后由:
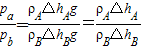 求得压强之比.
求得压强之比.解答:解:
(1)物体放入之前:pA=pB,hA=2hB;
即:ρAghA=ρBgh B;
所以:
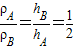 ;--①
;--①(2)物体放入之后,甲悬浮;
所以:V甲=V甲排;甲受到的浮力F甲=G甲;ρ甲=ρA;
由题知:乙物块所受浮力等于甲物块重力的一半;
所以:F乙=
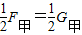 ;
;即:ρBV乙排g=
 ρAV甲排g;
ρAV甲排g; ;
;(3)由题知:放入物体之前,两柱形容器内装有A、B两种体积相同的液体;
所以:VA=VB;sAhA=sBhB;
即:
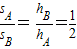 ;
;(4)根据排开液体体积的关系求深度变化的关系;
 ;
;即:
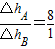 ;--②
;--②(5)根据上面①②两式得出压强变化之比:
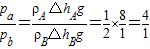 ;
; 故答案为:4.
点评:此题考查了液体压强的计算,难度较大,关键是找到比较压强变化的方法:即压强变化跟液体密度与深度变化的关系;公式多,计算复杂,这样难度的问题在近几年的中考中几乎不见了.

练习册系列答案
相关题目
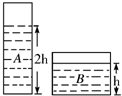 (2008?宣武区一模)如图所示,两柱形容器内装有A、B两种体积相同的液体,A液体深度是B 液体深度的2倍,两种液体对容器底部的压强相同.若将甲、乙两物块分别投入A、B两液体中,液体均未溢出,且甲物块在A中悬浮,乙物块密度是甲物块的3倍,乙物块所受浮力等于甲物块重的一半.则这时两容器底部所受液体的压强分别增加为pa和pb,则pa=
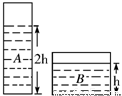
(2008?宣武区一模)如图所示,两柱形容器内装有A、B两种体积相同的液体,A液体深度是B 液体深度的2倍,两种液体对容器底部的压强相同.若将甲、乙两物块分别投入A、B两液体中,液体均未溢出,且甲物块在A中悬浮,乙物块密度是甲物块的3倍,乙物块所受浮力等于甲物块重的一半.则这时两容器底部所受液体的压强分别增加为pa和pb,则pa=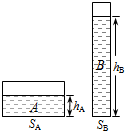 (2009?石景山区二模)如图所示,两柱形容器的底面积SA=3SB,容器内分别装有A、B两种液体,容器底受到的压强pA=pB.若将质量相等的甲、乙两物块分别投入A、B两液体中,液体均未溢出,且甲物块在A中悬浮,乙物块在B中沉底,甲物块密度是乙物块的3倍,这时液体A、B对容器底的压强分别增加了△pA、△pB,已知△pB=2△pA,那么,原容器内所装液体的高度之比hA:hB=
(2009?石景山区二模)如图所示,两柱形容器的底面积SA=3SB,容器内分别装有A、B两种液体,容器底受到的压强pA=pB.若将质量相等的甲、乙两物块分别投入A、B两液体中,液体均未溢出,且甲物块在A中悬浮,乙物块在B中沉底,甲物块密度是乙物块的3倍,这时液体A、B对容器底的压强分别增加了△pA、△pB,已知△pB=2△pA,那么,原容器内所装液体的高度之比hA:hB=