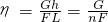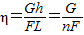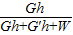题目内容
用滑轮组将重为G的物体匀速拉高h，滑轮组由n段绳承担总重，绳子自由端在拉力F作用下移动的距离为L，动滑轮共重为G′，克服绳重及摩擦所做的额外功为W，则（ ）
分析：A、掌握机械效率的概念，知道机械效率是有用功与总功之比，所以可利用公式机械效率η=
，来判断A是否符合题意．
B、总功等于有用功加额外功，所以可利用公式机械效率η=
=
，来判断B是否符合题意．
C和D、知道机械效率与物重、动滑轮的重力和绳重及摩擦的大小有关，来判断C和D是否符合题意．
| W有用 |
| W总 |
B、总功等于有用功加额外功，所以可利用公式机械效率η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额外 |
C和D、知道机械效率与物重、动滑轮的重力和绳重及摩擦的大小有关，来判断C和D是否符合题意．
解答：解：
从题可知，对物体做的功为有用功，W有用=Gh，
拉力F做的功为总功，W总=FL，
对动滑轮做的功为额外功，W额外=G′h，
克服绳重及摩擦所做的额外功为W，
A、滑轮组的机械效率为：η=
=
=
=
，故A符合题意．
B、滑轮组的机械效率为：η=
=
=
，故B符合题意．
C、此题滑轮组没有发生变化，所以在此过程中所做的额外功不变，由于货物的重力增加，所以有用功增大，由公式η=
可知，有用功在总功中所占的比值将增大，所以机械效率增大，故C符合题意．
D、机械效率与物重、动滑轮的重力和绳重及摩擦的大小有关，滑轮组的机械效率与承担物重的绳子段数无关，故D不符合题意．
故选A、B、C．
从题可知，对物体做的功为有用功，W有用=Gh，
拉力F做的功为总功，W总=FL，
对动滑轮做的功为额外功，W额外=G′h，
克服绳重及摩擦所做的额外功为W，
A、滑轮组的机械效率为：η=
| W有用 |
| W总 |
| Gh |
| FL |
| Gh |
| Fnh |
| G |
| nF |
B、滑轮组的机械效率为：η=
| W有用 |
| W总 |
| W有用 |
| W有用+W额外 |
| Gh |
| Gh+G′h+W |
C、此题滑轮组没有发生变化，所以在此过程中所做的额外功不变，由于货物的重力增加，所以有用功增大，由公式η=
| W有用 |
| W总 |
D、机械效率与物重、动滑轮的重力和绳重及摩擦的大小有关，滑轮组的机械效率与承担物重的绳子段数无关，故D不符合题意．
故选A、B、C．
点评：同时考查了有关机械效率的计算，一定要掌握机械效率的概念．在此题中还考查了影响滑轮组机械效率的因素，知道机械效率与物重和动滑轮的重力有关．
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
